Astuce concours #3

Dans le billet Astuce concours #2, j’insistais sur la sous-utilisation de la décomposition multiplicative dans la recherche du nombre-cible. Nos habitudes et notre culture éducative nous poussent plus vers d’autres décompositions, comme la distributivité de la multiplication sur l’addition.

Décomposition multiplicative vs distributivité

Il est juste de préciser que la distributivité fonctionne dans toutes les situations de décomposition alors que la décomposition multiplicative exclut les nombres premiers. Par contre, la distributivité n’est pas toujours pertinente donc ne devrait pas devenir une procédure choisie systématiquement.

Dans les explications de cette sous-utilisation, il y a aussi la conséquence indirecte de l’apprentissage des tables de multiplication trop axé sur le sens direct. 6×9 = ? qu’il faudrait systématiquement accompagné de la pratique à l’envers, 54 c’est quoi ?

Partir d’une solution simple puis la complexifier

L’épreuve 10 soumise aux classes de cycle 3 participantes au concours Mathador, permet de faire une analyse vraiment intéressante de la décomposition du nombre cible (54) puis de la complexification de façon à obtenir plus de points (en référence au système de points du concours).

Pour rappel, le système de points fonctionne de la manière suivante :

• Utilisation d’une addition ou d’une multiplication : 1 point
• Utilisation d’une soustraction : 2 points
• Utilisation d’une division : 3 points

Le nombre-cible 54 était à fabriquer en utilisant les cinq nombres 2 / 4 / 6 / 8 et 11

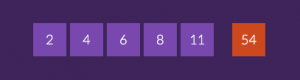
Évidemment la 1^ère décomposition qui vient à l’esprit est un 6×9.

Et résoudre l’épreuve s’avère assez simple : 11 – 2 = 9 et 9×6 = 54. Cette solution permet à l’élève de remporter 3 points.

Dans le cadre du concours, l’élève dispose de 4 minutes pour proposer sa solution. Que vous appliquiez vous aussi ces 4 minutes de réflexion dans le cadre d’une séance de calcul mental en classe avec Mathador ou un temps plus court, l’important est de guider les élèves pour qu’ils puissent bien gérer leur temps de réflexion.

Le conseil donné aux élèves pour bien gérer les 4 minutes est de chercher au tout début une solution simple puis de la complexifier ensuite.

Cette pratique s’applique ici à merveille ! En effet, le 6 étant donné dans les 5 nombres, comment fabriquer différemment le 9 avant d’effectuer ce 9×6 ?

1^ère possibilité :

4 – 2 = 2 puis 11 – 2 = 9 et 9×6 = 54 ; solution à 5 points

2^ème possibilité :

4:2 = 2 puis 11 – 2 = 9 et 9×6 = 54 ; solution à 6 points

3^ème possibilité :

8 – 4 = 4 puis 4 – 2 = 2 puis 11 – 2 = 9 et 9×6 = 54 ; solution à 7 points

4^ème possibilité :

8 – 4 = 4 puis 4:2 = 2 puis 11 – 2 = 9 et 9×6 = 54 ; solution à 8 points

Ces cinq solutions basées sur la complexification dans la fabrication du 9 mettent bien en évidence le travail sur le sens des opérations. Il y a en action dans cet exercice mental toute la richesse pédagogique du travail de la décomposition des nombres qui fait intervenir le sens des opérations, le sens des nombres avec en permanence la présence en arrière-plan des ordres de grandeur.

Une approche possible par tâtonnement

Pour compléter cette recherche de 54, il y avait aussi dans les solutions simples deux solutions basées sur une approche par tâtonnement.

D’abord 4×11 puis 44 + 8 et 52 + 2, solution à 3 points puis une approche supérieure à 54 :

6×11 puis 66 – 8 et 58 – 4 , solution plus intéressante à 5 points.

Enfin, il est à noter que le coup Mathador était difficile car imposait un passage par 4×15 = 60.

Soit 8:2 = 4 puis 4 + 11 = 15 puis 15×4 = 60 et 60 – 6 = 54.