Astuce concours #5

Pour ce dernier billet Astuce n°5 du concours 2016/2017, je vous propose une analyse approfondie de l’épreuve 14 du cycle 4.

A la lecture et correction des épreuves de ma classe de 5°, j’ai découvert avec plaisir qu’un des points sur lequel j’insiste depuis le début du concours avait été bien mis en action pour cet avant-dernier tirage.

En effet, j’ai eu l’occasion de l’écrire aussi dans d’autres billets du blog, il est important pour l’élève de chercher à décomposer le nombre-cible avant même de chercher à opérer sur les 5 nombres pour essayer de fabriquer cette cible.

Si une ou des décompositions simples sont possibles, une bonne piste consiste à essayer de fabriquer simplement et rapidement le nombre-cible. Avantage, j’ai trouvé une solution et je peux désormais essayer de complexifier mon calcul de façon à obtenir davantage de points ou éventuellement tester d’autres pistes.

Cette épreuve 14 du cycle 4, avec comme nombre-cible 77, est parfaite pour chercher à complexifier une décomposition simple de 77.

Cette analyse m’a aussi confirmé un autre paramètre important du concours et de Mathador. Pour trouver le nombre-cible, une solution comporte 1, 2, 3 ou 4 étapes. Disposant de 5 nombres, 4 est le nombre maximum de maillons de ma solution. Il est intéressant de constater que le passage de 2 à 3 ou 4 étapes semble un cap difficile à franchir pour de nombreux élèves. On peut faire un parallèle avec le principe de la démonstration en mathématique qui se complique avec le nombre de pas d’une démonstration.

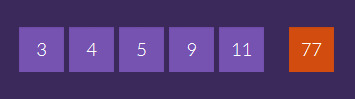
Le nombre-cible 77 était à fabriquer en utilisant les cinq nombres 3 / 4 / 5 / 9 et 11

Si vous êtes joueur… et c’est forcément le cas si vous lisez ce billet ! Je vous propose de prendre quelques minutes pour chercher le plus de décompositions menant à 77, avant de découvrir les 8 propositions ci-dessous qui proviennent d’une classe de 5°. Top chrono, c’est parti !

L’unique décomposition multiplicative de 77 est 7×11.

• 1^ère possibilité :

3 + 4 = 7 puis 7×11 = 77 ; solution à 2 points

Plus de la moitié des élèves de la classe de 5° ont validé cette solution.

Toutes les propositions qui suivent ont été proposées par au moins un élève.

• 2^ème possibilité :

5 – 3 = 2 puis 9 – 2 = 7 et 7×11 = 77 ; solution à 5 points

• 3^ème possibilité :

3 + 4 = 7 puis 5 + 9 = 14 puis 14 – 7 = 7 et 7×11 = 77 ; solution à 5 points

• 4^ème possibilité :

9:3 = 3 puis 3 + 4 = 7  et 7×11 = 77 ; solution à 5 points

• 5^ème possibilité :

5 – 3 = 2 puis 9 + 2 = 11 puis 11 – 4 = 7 et 7×11 = 77 ; solution à 6 points

• 6^ème possibilité :

5 – 3 = 2 puis 4 – 2 = 2 puis 9 – 2 = 7 et 7×11 = 77 ; solution à 7 points

• 7^ème possibilité :

5 – 4 = 1 puis 3 – 1 = 2 puis 9 – 2 = 7 et 7×11 = 77 ; solution à 7 points

• Et enfin le coup Mathador, trouvé par un élève de la classe, encore sur le principe enrichi de 7×11 :

5 + 3 = 8 puis 8:4 = 2 puis 9 – 2 = 7 et 7×11 = 77 ; coup Mathador à 13 points

Dans ces huit décompositions enrichies de 7×11, et la liste n’est pas exhaustive, on retrouve toute la richesse pédagogique du travail sur la décomposition des nombres qui fait intervenir le sens des opérations, le sens des nombres avec la présence en arrière-plan des ordres de grandeur. L’étendue des différents chemins pour fabriquer 77 avec leurs différences en complexité est un atout fort pour permettre à tous les élèves, même ceux qui sont en difficulté, pour rentrer dans ce type de raisonnement producteur de sens.

Maintenant que le concours se termine, pour entretenir cette gymnastique, on peut imaginer de proposer en classe des situation comme ce 77 et en conseillant aux élèves de tester cette démarche qui consiste à partir d’une décomposition très simple, de chercher à la complexifier.