Calcul mental en classe : le concours Mathador

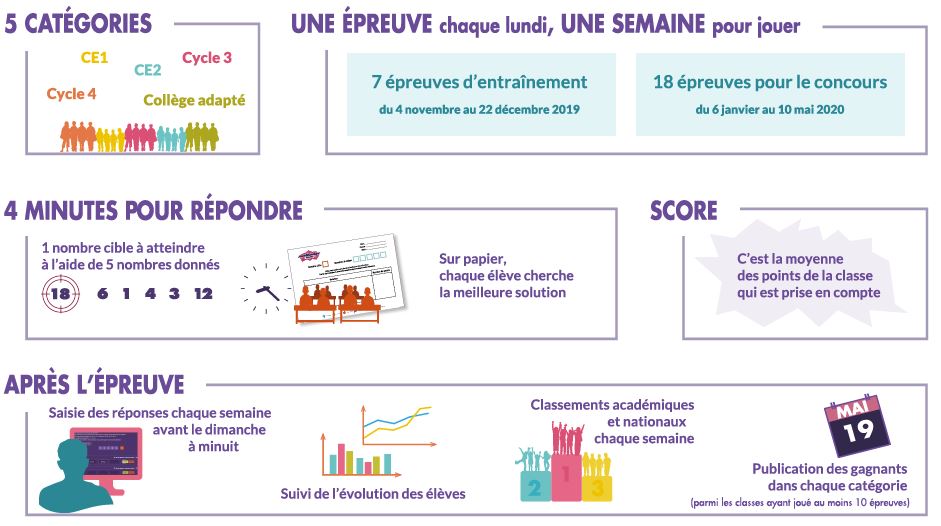
Le concours 2020 a débuté le 6 janvier. Un travail de mentalisation de la relation aux nombres et aux opérations a été mis en place au cours de la période de septembre à décembre avec des diaporamas, les jeux Trio et Mathador, et les tirages d’entraînement. Ce concours est un outil supplémentaire pour faire vivre la régularité de ces pratiques mentales.

 

Pourquoi participer au concours Mathador ? 

Le concours Mathador met l’élève en situation de recherche chaque semaine avec un nombre-cible à fabriquer. Cette étape est l’occasion pour l’élève d’utiliser ses connaissances automatisées. Pour améliorer son total de points, l’élève va régulièrement tester de nouvelles pistes. C’est alors un moment de construction de nouvelles connaissances qui nécessiteront certainement de la répétition avant de devenir des automatismes. Lors de cette période, il cherche, calcule, raisonne, modélise et communique, soit la mise en œuvre de cinq des six grandes compétences mathématiques.

De façon complémentaire à ces tests de l’élève, et pour lui ouvrir de nouveaux horizons, la phase d’analyse des procédures qui suit un tirage, est une étape très importante. Si l’étape de recherche s’inscrit dans les phases Régularité et Répétition, l’analyse présentée à toute la classe la semaine suivante par le professeur concerne la phase Verbalisation. On retrouve le triptyque RRV : Régularité-Répétition-Verbalisation. Cette troisième étape de verbalisation est le moment où l’élève qui a cherché et qui a déjà ses propres repères va découvrir des pistes nouvelles, auxquelles il n’aurait peut-être pas pensé seul. Cette phase de verbalisation est essentielle dans la construction du sens du nombre et des opérations.

 

Le concours 2019/2020 en quelques chiffres

Environ 2000 classes participantes :

CE1 : 100 classes

CE2 : 250 classes

Cycle 3 : 1100 classes

Cycle 4 : 500 classes

Collège adapté : 50 classes

Le nombre de classes inscrites augmente régulièrement tous les ans depuis le lancement il y a 5 ans, et il peut encore augmenter en début d’année 2020 car il est possible de prendre le concours en marche. Mais pour être sur le podium final, il ne faut pas trop tarder. En effet, chaque classe a besoin de participer à 10 épreuves pour figurer dans le classement. Le concours se termine le 10 mai, ce qui peut paraître lointain, mais aucune épreuve n’a lieu pendant les vacances. Le calendrier va donc filer assez vite.  

Le concours #Mathador 2020 est officiellement ouvert : la première épreuve est disponible 🎉
Vous pouvez encore vous abonner à Mathador classe par ici 👉https://t.co/aa8udNqnrk #calculmental #maths #pédagogie pic.twitter.com/3VrjLDym8L

— Mathador (@Mathador) January 6, 2020

 

L’importance des objectifs

Évidemment, comme dans tout concours, chacun souhaite réussir le mieux possible et pourquoi pas gagner. Mais, étant donné le nombre très important de classes participantes, on comprend très vite que l’objectif du podium ne peut être l’unique finalité puisqu’il ne peut être atteint chaque semaine que par quelques classes participantes !

L’originalité du concours est de mêler du collectif avec de l’individuel. Le classement est collectif, mais la réflexion et le travail sont individuels. Je pense qu’il faut recentrer les objectifs sur chacun des élèves et notamment fixer comme premier but à chacun d’essayer de trouver une solution simple, et de le faire au début de la recherche des 4 minutes. 

Il est important de conseiller aux élèves, une fois que le nombre-cible est fabriqué, de commencer à chercher des solutions plus complexes, c’est-à-dire en utilisant les soustractions et des divisions. Il faut aussi conseiller aux élèves d’écrire plusieurs solutions sur leur feuille. Il faut alors compter les points et sélectionner la solution avec le plus de points. Le coup Mathador n’est évidemment pas l’objectif majeur, il ne peut concerner que quelques élèves puis petit à petit d’autres élèves au fur et à mesure des progrès.

Un des objectifs pédagogiques de Mathador et de son système de points est d’inciter à utiliser la soustraction et la division de façon à les rendre plus naturelles.

Les tirages sont conçus de façon à contenir des solutions simples en 1 ou 2 lignes, mais aussi des solutions en 3 ou 4 lignes de calcul et systématiquement au moins un coup Mathador. Une technique efficace consiste à partir d’une solution simple puis à la complexifier en se servant des nombres qui restent.

 

Analyse de solutions à la suite du tirage 1 en cycle 3

Prenons en exemple le 1^er tirage du concours du cycle 3 :

Le conseil à donner régulièrement aux élèves est de partir du nombre-cible et de se demander, comment le fabriquer. En clair, dans le répertoire personnel de l’élève, l’inciter à rechercher dans ses connaissances automatisées mais aussi réfléchies, des pistes pour fabriquer 30, une façon d’enclencher la mécanique du calcul à l’envers, très riche en construction de sens du nombre et des opérations mais pas naturelle, d’où l’importance de la susciter régulièrement chez nos élèves.

Parmi les solutions que la plupart des élèves de cycle 3 doivent retrouver dans leur répertoire, il y a 3 x 10 et 6 x 5. Il faut leur donner le conseil d’observer ensuite dans la liste des 5 nombres si la décomposition envisagée est  intéressante ou non. Dans le cas présent, le 3 x 10 est simple et le 6 x 5 est envisageable.

 

Voici quelques solutions de mes élèves de 6ème lors de ce tirage 1 

Autour de l’idée de 3 × 10 :

11 – 1 = 10 puis 3 × 10 = 30 (solution en 8 points : 5 + 2 + 1, trouvée par 4 élèves)

Cette solution présentait l’intérêt de pouvoir s’enrichir pour donner un coup Mathador :

4 : 2 = 2 ; 11 – 2 = 9 puis 9 + 1 = 10 puis 3 × 10 = 30 (Mathador donc 18 points, trouvés par 3 élèves)

La plupart des élèves ont commencé par 11 × 3 = 33 et ont cherché à ajuster pour trouver 30. Voici les 5 solutions que j’ai pu lire :

11 × 3 = 33 ; 33 – 2 = 31 puis 31 – 1 = 30 (solution en 10 points : 5 + 1 + 2 + 2, trouvés par 7 élèves)

11 × 3 = 33 ; 33 – 4 = 29 ; 2 – 1 = 1 puis 29 + 1 = 30 (solution en 11 points : 5 + 1 + 2 + 2 + 1, trouvée par 5 élèves)

11 × 3 = 33 ; 2 – 1 = 1 ; 4 – 1 = 3 puis 33 – 3 = 30 (solution en 12 points : 5 + 1 + 2 + 2 + 2, trouvée par 1 élève)

11 × 3 = 33 ; 4:2 = 2 ; 33 – 2 = 31 puis 31 – 1 = 30 (solution en 13 points : 5 + 1 + 3 + 2 + 2, trouvée par 1 élève)

11 × 3 = 33 ; 4:2 = 2 ; 2 + 1 = 3 puis 33 – 3 = 30 (Mathador donc 18 points, trouvés par 3 élèves)

À noter que l’autre décomposition de 30 en 6 × 5 n’a été proposé par aucune élève. Il est vrai qu’il fallait penser à fabriquer le 5 et le 6. Par exemple : 2 × 6 = 6 ; 4 + 1 = 5 puis 6 × 5 = 30

En calcul mental comme dans de nombreux autres domaines, l’être humain a tendance à reproduire ce qu’il pense maîtriser sans forcément chercher d’autres procédures, tout simplement par habitude et confort. Il est donc essentiel de proposer des bilans des solutions trouvées dans la classe au tirage précédent. Il ne faut pas forcément tout présenter, mais un échantillon représentatif éventuellement en les personnalisant, les élèves apprécient. L’idée de complexifier une solution de base comme les exemples ci-dessus est à présenter de temps en temps, car ce n’est pas une démarche naturelle de raisonnement pour de nombreux élèves. 

Cette présentation de différentes procédures permettra dans la durée d’enrichir le répertoire personnel de chacun en faisant vivre la diversité des approches et des décompositions et donnera des idées pour les tirages suivants. C’est aussi une façon de sortir de l’image binaire du calcul, à savoir « une opération, un résultat ». C’est une des forces pédagogiques du calcul à l’envers de proposer de nombreuses pistes et donc de ne pas se limiter à « je sais où je ne sais pas » où « j’ai juste ou j’ai faux » !

Cela suscite généralement des échanges dans la classe. C’est un excellent complément avec les phases de verbalisation et d’échanges pratiquées pendant les diaporamas de calcul mental.

 

Les statistiques du concours Mathador

Lorsque 3 ou 4 tirages auront été effectués, les statistiques de chaque élève sont à la disposition du professeur. En complémentarité des séances collectives d’analyse de procédures qui permettent à chacun d’enrichir son répertoire, il est aussi intéressant de montrer à chaque élève ses propres statistiques. Chaque enseignant a accès sur son compte personnel à de nombreux indicateurs de suivi du concours de sa classe. Certains paramètres sont collectifs avec des comparatifs des moyennes de classe avec les classements nationaux et académiques. 

D’autres concernent l’évolution de chaque élève de la classe avec notamment son résultat à chaque tirage : nombre de points et comparatifs visuels par histogramme avec les moyennes nationales et académiques. On retrouve aussi un diagramme circulaire de la répartition en pourcentages de l’utilisation des quatre opérations. Il sera intéressant de montrer plusieurs fois à chaque élève pendant la période du concours l’évolution de ses résultats de façon à lui faire prendre conscience de quelques indicateurs le concernant. C’est l’occasion d’échanger quelques mots et surtout de mettre en évidence les points forts et les points faibles et de lui donner des conseils pour la suite des épreuves du concours.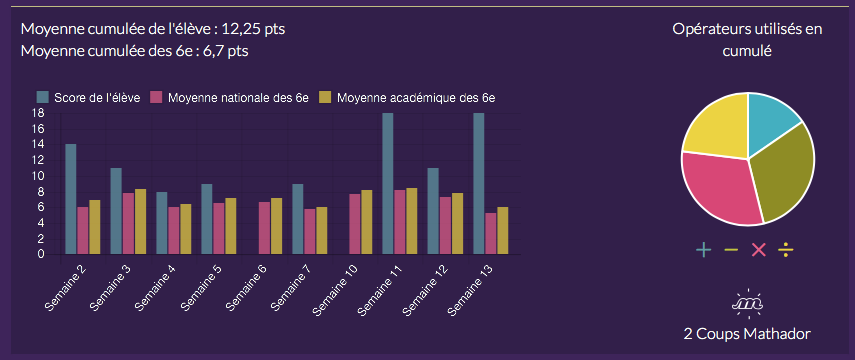

Bon concours à tous !