Le calcul mental en 6° – semaine 19
L’alternance entre la salle multimédia et le travail en salle de classe est désormais bien en place ! D’un côté, une relation plus solitaire avec l’ordinateur et ses retours immédiats, de l’autre, une dimension sociale plus forte avec des échanges au sein du collectif !
Zoom sur Quadricalc !
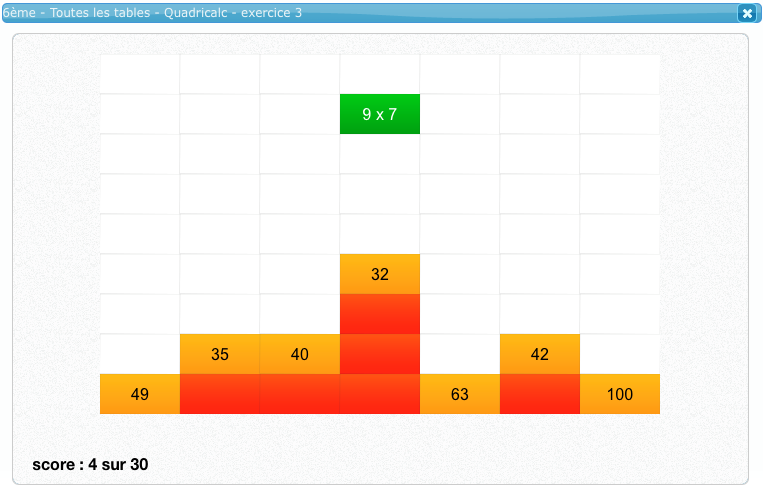
Du côté de la salle multimédia, un jeu sur Calcul@TICE rencontre un grand succès auprès des élèves : Il s’agit de Quadricalc qui est tout simplement un « Tétris » avec des opérations. Il suffit, avec les flèches du clavier, de viser la bonne réponse avec la brique qui descend. La dimension ludique est évidente et c’est un travail de consolidation des connaissances automatisées. Quadricalc se retrouve dans chaque niveau du CP à la 6ème avec, à chaque fois, 4 niveaux de difficultés de vitesse de descente de la brique. Il est donc possible d’adapter à chacun le niveau de jeu avec les opérations travaillées, notamment le registre additif ou multiplicatif. C’est encore une fois la répétition et la régularité qui permettra d’installer une aisance et au fil du temps de progresser dans les niveaux.
Concours Mathador : point sur les statistiques individuelles
La configuration de la salle multimédia me donne la possibilité de montrer à chaque élève ses statistiques personnelles du concours après les quatre premiers tirages. Il est important de pouvoir les montrer à chacun en l’absence du regard des autres. Chacun passe environ une minute à mon pupitre et l’on découvre ensemble les statistiques. J’insiste sur quelques indicateurs : déjà les résultats de la classe puis la moyenne de points de l’élève en comparaison avec la moyenne nationale. Ensuite, on regarde les histogrammes de chacun des tirages avec les trois rectangles (élève, national, académique). Enfin, j’aime bien montrer à chacun la répartition des opérations choisies entre l’addition, la soustraction, la multiplication et la division : le diagramme circulaire est très parlant.
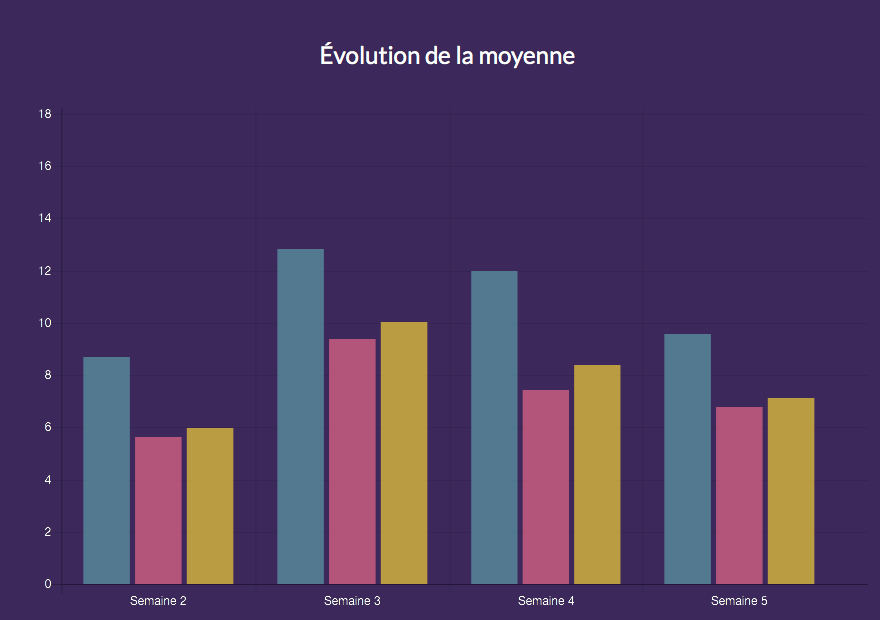
Les statistiques d’un élève très fort en calcul mental, il a déjà réalisé 3 coups Mathador lors des 4 premiers tirages :
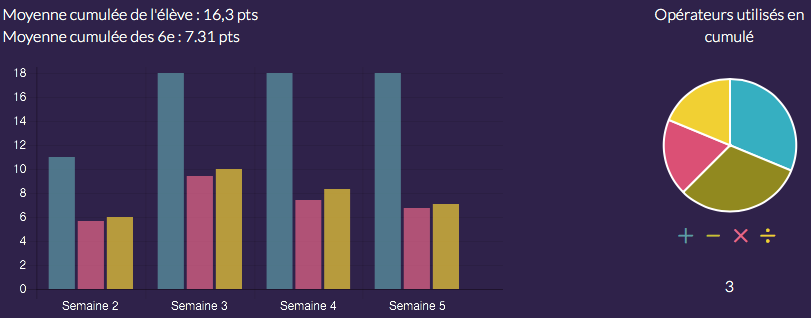
Enfin un élève en difficulté avec les nombres et les opérations :
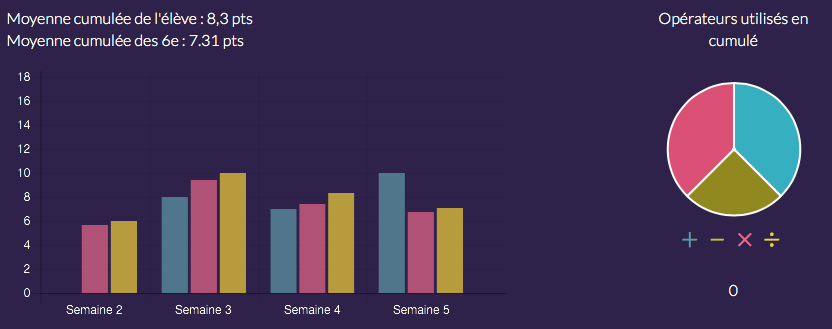
Relation aux décimaux : évaluation
Retour en salle de classe ! Environ à la moitié de l’année scolaire, j’ai donné une évaluation ( Eval3-022018 ) afin de vérifier où se situait la relation aux décimaux. Bien installée pour les élèves qui réussissent à bien jongler avec les entiers à Trio ou Mathador, cette relation mentale aux décimaux est encore en phase de construction pour de nombreux élèves. Toutefois, l’ensemble des résultats est encourageant et tous les élèves sont dans le processus, c’est important !
Retour sur l’épreuve n°3 du concours
Quelques retours cette fois sur le tirage n°3 du cycle 3 :

C’est un tirage intéressant car riche en solutions diverses. Je vous propose un zoom sur une analyse qui s’appuie sur la décomposition multiplicative de 40. Il faut régulièrement aborder cette notion de décomposition multiplicative de façon à la rendre naturelle : ce n’est pas le cas pour tous les élèves ! D’où l’importance de procéder, en classe, à une analyse des différents chemins possibles d’un tirage. Revenons à notre nombre cyble pour lequel deux pistes viennent rapidement à l’esprit : 5×8 ou 4×10.
Concernant le 5×8, 5 étant donné, il suffisait de fabriquer un 8. Deux pistes 10–2 ou 9–(2:2). Dans le premier cas 5x(10–2) rapportait 8 points et le second 5x(9–(2:2)) 11 points. Parmi mes élèves, c’est l’autre décomposition 4×10 qui a eu du succès.
La particularité de ce tirage est d’offrir une palette très large de solutions basées sur 4×10 partant d’une solution à 7 points pour terminer par un coup Mathador à 18 points. Le principe est de partir d’une décomposition simple est de la complexifier petit à petit de façon à la bonifier avec le système de points :
(2+2)x10 rapporte 7 points 2+2=4 ; 4×10=40
(9-5)x10 8 points 9-5=4 ; 4×10=40
(9-5)x10+2-2 11 points 9-5=4 ; 4×10=40 ; 40+2=42 ; 42-2=40
(9-5)x10x2:2 12 points 9-5=4 ; 4×10 ; 40×2=80 ; 80:2=40
(9-5)x10:(2:2) 14 points 9-5=4 ; 4×10=40 ; 2:2=1 ; 40:1=40
Enfin le coup Mathador à 18 points :
9-5=4 ; 4:2=2 ; 2+2=4 ; 4×10=40 ((9-5):2+2)x10=40
Ce coup Mathador ne présente aucune difficulté calculatoire mais nécessite un très bon sens des opérations et une connaissance fine des décompositions de façon à pouvoir construire un 4 avec 2/2/5 et 9 et en utilisant une addition, une soustraction et une division. L’analyse ci-dessus est intéressante à montrer aux élèves pour leur donner de nouvelles pistes et construire une relation réfléchie aux nombres et aux opérations. Comme je l’ai déjà évoqué dans le dernier billet, il est important de préciser que le coup Mathador n’est pas l’objectif pour tous les élèves. De toute évidence, celui-ci est hors de portée de nombreux élèves. L’objectif majeur reste d’atteindre le nombre-cible et progressivement d’enrichir ses solutions. Les avancées et les progrès se font dans la durée, progressivement, avec une alchimie de consolidation de ses acquis et d’enrichissement de nouvelles approches. Avec bien sûr la touche de plaisir qu’apportent le jeu et le concours !