Le calcul mental en 6° – semaine 17
Le concours Mathador est cette fois bien lancé ! Les échanges entre les élèves contribuent à la création d’une relation aux nombres et aux opérations plus forte. La régularité mise en place avec ce tirage doit permettre l’installation de ce répertoire numérique et opératoire que chaque élève doit se construire.
En avant pour la seconde épreuve !
Le second tirage en catégorie cycle 3 était plus accessible que le premier concernant les coups Mathador. Par contre, il présentait aussi une grande diversité de solutions avec de nombreuses solutions simples…
Lundi, fin de l’heure, ce sera notre rituel de début de semaine : je distribue deux petites feuilles, une feuille vierge pour le second tirage accompagnée de la feuille du premier tirage. Nous avons fait une analyse du premier tirage la semaine dernière en partant de la base 15+11 qui pouvait permettre d’atteindre 28 de 4 façons différentes en 9 ; 10 ; 11 ou 12 points. Cette analyse était collective, je les avais prévenu que je leur redonnerais leur feuille de calculs juste avant le prochain tirage, de façon à vérifier leur total de points. C’est aussi une façon de minimiser les loupés, c’est-à-dire les zéros, de quelques élèves et de rester dans la dimension collective du tournoi. J’aborde oralement les erreurs commises, notamment la réutilisation d’un nombre ou quelques erreurs de calculs mais il me semble important de ne pas nommer ces élèves devant le groupe afin d’éviter de les mettre dans une situation difficile de façon totalement inutile ! J’insiste même sur le fait que l’erreur de « calcul bête » ou la réutilisation d’un nombre guette chacun d’entre nous et que sur l’ensemble du concours, beaucoup d’élèves de la classe seront concernés au moins une fois. Et j’ajoute, « soyez bien vigilant ! ». Avant d’écrire au tableau le second tirage, la tension monte ! Je leur rappelle la consigne importante : bien gérer les 4 minutes et commencer par chercher une solution simple avant de rentrer dans la phase de complexification des calculs. Je leur reprécise également que chaque tirage contient toujours au moins un coup Mathador.
Et je termine avec une remarque sur le coup Mathador : ce n’est pas un objectif principal pour tous les élèves ! Il faut déjà trouver une solution simple et seulement ensuite s’intéresser au coup Mathador. L’objectif majeur est de trouver une solution !
C’est parti pour le tirage !
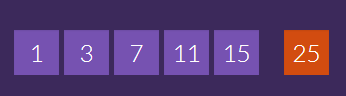
4 minutes de gymnastique des neurones. Hasard : on retrouve le 11 et le 15, déjà présents dans le 1er tirage ! Le 26-1 sera une bonne porte d’entrée pour mettre en application la consigne de trouver une solution facile.
Les 4 minutes sont écoulées, je ramasse les feuilles sans échange avec le voisin, nous n’avons pas le temps. Comme lors du premier tirage, certains élèves calculent et écrivent sur leur feuille leur total de points. Les échanges entre les élèves à la sortie de la classe annoncent des coups Mathador qui seront confirmés lors de la correction.
Grande diversité des résultats
Pour une grande majorité, la solution facile n’a pas été 11+15-1 mais plutôt 15+7+3. Confirmation, le cerveau préfère le chemin direct de l’addition à la soustraction ! Ce 15+7+3 avait aussi un intérêt majeur, la possibilité de diviser par 1. L’automatisation du divisé par 1 est en marche ! Beaucoup de propositions de cette solution (15+7+3):1 que les élèves doivent présenter en 3 lignes : 15+7=22 ; 22+3=25 ; 25:1 = 25 ou 7+3=10 ; 10+15=25 ; 25:1=25. Intérêt, elle rapporte 10 points au lieu des 7 points du 15+7+3.
Ce 2ème tirage était vraiment intéressant pour ces solutions simples mais aussi pour ces coups Mathador relativement accessibles. J’ai eu le plaisir d’en corriger quelques-uns et deux différents. En cherchant à se rapprocher de 25, la connaissance des tables et les ordres de grandeur ont incité quelques élèves à commencer par 3×7=21 et la suite conduit assez simplement vers un coup Mathador avec 15-11=4 puis 21+4=25 et enfin la division par 1. Ce coup Mathador a rencontré du succès. Toujours dans l’idée de s’approcher de la cible avec la notion d’ordre de grandeur, j’ai lu aussi, 3×11=33 puis 33+7=40 puis 40-15=25 et toujours le divisé par 1 pour terminer. Joli, moins intuitif que le premier car le cerveau semble plus facilement trouver un complément à ajouter qu’à enlever pour atteindre le nombre-cible. En effet, 25 se conçoit plus aisément en 21+4 qu’en 33-8.
Il est toujours intéressant de prendre un moment dans la semaine suivante du tirage pour présenter une palette des solutions possibles toujours dans l’idée de constituer ce répertoire et de remplir la trousse à outils nombres-opérations de nos élèves. Je présenterai peut-être aux élèves un coup Mathador basé sur la décomposition multiplicative de 25 en 5×5, un peu dans le même registre que celui du tirage 1 où il fallait passer par 4×7 pour fabriquer 28. Ici, un premier 5 provient de 15:3=5 et le deuxième 5 provient de 11-7+1=5 et on termine par la multiplication 5×5. Ce coup Mathador est évidemment difficile pour des élèves de cycle 3 mais il est très riche d’un point de vue pédagogique.
Le travail régulier en calcul mental se poursuit…
Je mets en place depuis quelques semaines une alternance entre la salle multimédia et le travail en classe avec les séries mentales en diaporama. En salle multimédia, trois sites seront mis en avant : Mathenpoche, Calculatice et Mathador (3 sites à mettre en lien).
Dans Mathenpoche, la partie calcul mental de la rubrique « Entiers et opérations » est constituée de 15 exercices avec une progression dans la difficulté de l’addition vers la division. Ces 15 exercices forment un bel ensemble à pratiquer régulièrement en échauffement. Je leur permets de passer d’un exercice à l’autre dès qu’ils ont 5 bonnes réponses, le fonctionnement du site est de 10 questions par niveau.
Ensuite, les élèves peuvent jouer sur Calculatice et Mathador Chrono. Depuis quelques semaines, ils ont une feuille de scores que je leur remets en salle multimédia et je la conserve d’une séance à l’autre. Ils doivent noter les jeux et les scores effectués sur Calculatice puis à Mathador Chrono. Dans le billet 6, j’avais présenté le site Calculatice et quelques-uns des jeux axés sur le calcul mental direct : une opération-un résultat. Ils peuvent choisir 3 ou 4 jeux dans la rubrique 6°. Ensuite, quelques parties de Mathador Chrono permettent de jouer sur dans le registres du calcul à l’envers avec la recherche du nombre-cible. La feuille de score individuel va permettre à chacun de mesurer son évolution. Le score d’une partie Mathador Chrono est une mesure de l’aptitude en calcul mental à l’envers. L’évolution sur l’ensemble d’une année scolaire est un indicateur pédagogique intéressant. Pour donner quelques repères, en-dessous de 50 points, la relation aux nombres et aux opérations est encore difficile, entre 50 et 100 points, on peut parler de relation en construction avec encore des fragilités. Franchir la barre des 100 points régulièrement est la traduction d’une bonne maîtrise des nombres et des opérations. Parmi mes classes de 6°, quelques élèves se situent régulièrement entre 150 et 200, c’est un très bon niveau. La régularité au-delà de 200 points, niveau difficile pour le cycle 3, est le début de l’excellence. Dépasser régulièrement les 300 ou 400 points est un niveau extraordinaire que très peu atteignent. Un billet récent du blog présente un supercalculateur qui a atteint ce niveau (à mettre en lien).
Quelques retours sur les échanges des dernières séries de calcul mental 19 et 20 !
Dans la série 19-6° à l’oral, les échanges autour des erreurs sur les calculs de décimaux sont toujours intéressants. Notamment, dans le calcul de la différence 5 – 3,45 qui pose encore problème pour des élèves. Pour ces élèves, il est important de les inciter à procéder mentalement par complément, sur le principe du rendu de monnaie à la boulangerie de 3,45€ à 5€. Le registre mental de la soustraction doit s’appuyer sur l’addition lorsque la fragilité est encore bien présente. Raisonnement que l’on va retrouver dans la question 5 de l’opération à trou « 12,5 – ? = 8,4 » Il est plus simple de trouver le complément entre 8,4 et 12,5. Cette agilité mentale est indispensable pour rentrer ensuite dans des recherches plus complexes où le sens des opérations et la compréhension du cadre et du texte sont entremêlés.
La série 20-6° est réalisée à l’écrit sur le petit cahier. La question sur la décomposition d’un nombre en somme, différence, produit et quotient concerne pour la première fois, avec les 4 opérations, un nombre décimal : 7,5. Cette gymnastique, qui constitue les prémisses du calcul mental à l’envers, se met progressivement mais sûrement en place. Une première dans cette série, l’introduction d’un calcul en plusieurs étapes avec des priorités de parenthèses. La question 4 « 5x(38 – 18) » ne pose pas de problème particulier car l’ordre d’écriture et de lecture est en correspondance avec les règles prioritaires. La question 5 (cinq fois la somme de six et de sept) est plus difficile car elle associe la compréhension de la langue qui perturbe justement cet ordre. Dans ce cas, le fait de pouvoir écrire est une aide indispensable en 6°.
Un petit mot sur le tirage Mathador de la dernière question : après le nombre-cible 95 de la série 18, dans cette série 20, c’est 98. Il faut, de temps en temps, dépasser les tables de multiplication pour travailler de nouveaux ordres de grandeur. Dans le cas présent, 7×13 permet de se rapprocher puis de fabriquer 98. Il est ensuite intéressant de montrer aux élèves que 98, c’est aussi 7×14 et cela peut donner un beau coup Mathador avec 13 + 6:2 – 2 pour fabriquer le 14 !