Et les dys…
Un élève dyscalculique a des difficultés, plus ou moins importantes, pour donner du sens et établir des liens avec les objets mathématiques avec lesquels il travaille. En fait, cette question centrale du sens en mathématiques a juste plus d’acuité pour ces élèves, mais la relation aux nombres et aux opérations nous concerne tous.
Des supports concrets pour visualiser, manipuler, toucher et verbaliser sont des réponses à ces difficultés de sens, car elles mettent en lien les mathématiques avec nos cinq sens ! Lorsqu’on joue, on manipule, on visualise, on échange. En fait, l’élève devient acteur par l’activation des trois sens principaux de l’apprentissage (toucher, vue, ouïe). Cette activité cérébrale est alors créatrice de sens et facilite l’acquisition de connaissances. Et voilà l’explication de l’extraordinaire apport du jeu en pédagogie, en particulier pour les dyscalculiques mais également pour tous les élèves. De plus, le jeu est fédérateur et par la dimension plaisir, il permet aussi d’évacuer le stress que le mot mathématique génère souvent.

Rapprochons-nous des nombres et des opérations !
Le calcul pratiqué à l’école est souvent à l’endroit, c’est-à-dire « une opération donnée, un résultat attendu ». Cette pratique, en phase avec la vie courante, n’est pas créatrice de sens car elle ne permet pas de créer des liaisons, des réseaux entre les nombres. Elle est vécue par l’élève comme un contrôle de connaissance, et par ce fait, cela binarise la relation aux nombres et aux opérations : je sais ou je ne sais pas !
Pour sortir de ce cadre, en complément, rien de mieux que les situations de calcul à l’envers : le principe universel du compte est bon. Et nous voilà dans l’univers du jeu : un nombre-cible à fabriquer et des nombres-outils pour calculer et tenter d’atteindre ce nombre-cible en les combinant avec les 4 opérations. L’élève devient acteur, donc joueur, car il doit faire des choix de nombres et d’opérations pour fabriquer la cible. Il teste, il tâtonne, il peut se tromper. On sort de la binarité des situations de calcul à l’endroit, le « ça fait combien ? ». Et en plus, il y a souvent plusieurs chemins possibles, ça devient intéressant, on va pouvoir échanger sur les différentes procédures et apprendre par la découverte de nouvelles connaissances.
Cette gymnastique est contre-nature car elle va à l’encontre du formatage de nos cerveaux lié à la culture ancestrale du « ça fait combien ? ». Elle est donc, dans un premier temps, difficile. Mais la régularité, la répétition de situations de calcul à l’envers est une clé pour commencer à installer une relation véritable avec les nombres et les opérations.
Les dimensions ludique et combinatoire du principe du compte vont permettre de donner plus de sens à cette relation car cela nous met en phase avec le fonctionnement du cerveau qui adore la gymnastique combinatoire, comme on peut le constater avec les millions d’adeptes des mots croisés, mots fléchés…
Cette gymnastique du compte est bon, est excellente car elle facilite la création de liaisons opératoires entre les nombres et permet de construire petit à petit son propre répertoire mental, sorte de caisse à outils rempli de liaisons de nombres et d’opérations. Fabriquer des réseaux, un peu à l’image de notre cerveau avec ses réseaux neuronaux, voilà ce qui se cache derrière cette pratique pédagogique ludique. Et le prolongement naturel de l’utilisation de cette caisse à outils est la résolution de problème, la finalité en mathématiques.
Mathador, un jeu pour faire parler les nombres et s’en faire des amis !
Avant de présenter Mathador et son utilisation pédagogique possible, quelques mots sur les jeux à mettre en place en amont car avec Mathador, le nombre-cible est entre 0 et 99 et il y a 5 nombres-outils entre 1 et 20. Et, même si il y a toujours possibilité d’adapter le niveau en limitant la taille des nombres, ce peut être déjà difficile pour un élève avec une dyscalculie forte car la combinatoire est importante. Des jeux comme « Shut the box », « Duo », « Trio » ou « Détective Mathéo » sont une excellente porte d’entrée dans l’univers du compte est bon car les nombres en jeu sont plus petits et la combinatoire est plus limitée.
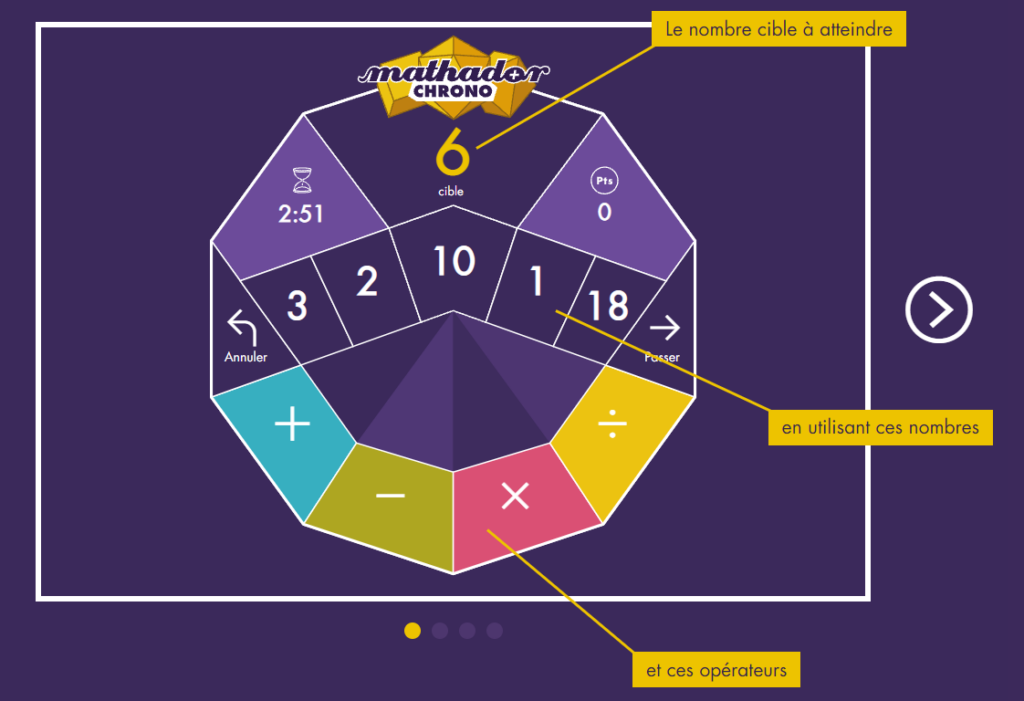
Revenons à Mathador ! Au départ, c’est la rencontre avec les solides de Platon, les 5 polyèdres réguliers à 4 ; 6 ; 8 ; 12 et 20 faces. Ce principe de base de Mathador se résume en deux phrases : un nombre-cible entre 0 et 99, il est déterminé par le lancer des deux dés rouges. Pour fabriquer ce nombre-cible, les joueurs disposent de 5 nombres outils qui sont déterminés par le lancer des 5 dés blancs, les solides de Platon, et des 4 opérations (addition, soustraction, multiplication et division) ! On ne peut utiliser un nombre qu’une fois et il n’y a pas obligation de tous les utiliser, l’utilisation des opérations est libre.
Ces dés polyédriques sont extraordinaires. Ils ont traversé les millénaires et continuent à rouler tranquillement devant nous. On a retrouvé des tétraèdres (le dé à 4 faces) dans des tombeaux égyptiens.
Cette magie du dé, qui attire tous les bambins et les grands, s’explique en partie par la fascination de le voir rouler et d’attendre impatiemment sur quel nombre il va s’arrêter. C’est un peu le mystère en mouvement sous nos yeux…
Le dé est aussi un des rares objets qui nous permet d’avoir un contact physique avec le nombre. On a l’impression de pouvoir toucher le nombre, être abstrait, présent autour de nous souvent en dimension 2, car écrit et à plat. Le dé permet au nombre de rentrer dans notre monde en 3D !
Un exemple en situation du jeu Mathador Flash !
En classe, deux possibilités de fonctionnement : soit le tirage, préalablement photographié, est vidéo-projeté sur le tableau à l’aide d’un diaporama ou alors, le lancer de dés est effectué en classe par les élèves et les nombres écrits au tableau par le professeur. Il faut alors laisser 3 à 4 minutes de recherche avec possibilité d’écrire sur le cahier ou l’ardoise. La recherche peut se faire en individuel ou en petits groupes. L’écrit répond alors à un besoin. Il faut, bien sûr, demander une écriture en ligne des opérations et sortir des techniques opératoires.
La différenciation est naturelle par le fait que chacun calcule avec ses connaissances et ses habitudes. Un élève en difficulté dépassera difficilement 2 lignes de calcul. Puis, avec un peu d’aisance, de fluidité mentale et d’entrainement, arriveront les solutions en 3 lignes et 4 lignes de calcul, puis, plus tard, les coups Mathador.
Pour découvrir et s’approprier un nouveau raisonnement, un élève doit l’entendre. Un élève qui verbalise son raisonnement ou sa procédure, met un haut-parleur sur sa pensée et le diffuse dans la classe…
Dans cette période d’échanges et d’explicitation des différentes procédures, par verbalisation, avant l’écriture au tableau, chacun va pouvoir découvrir de nouvelles pistes. C’est là que les deux piliers « Régularité » et « Répétition » rentrent en scène et vont permettre aux découvertes, dues à la verbalisation et aux échanges, de devenir de nouveaux apprentissages. L’écriture de différentes solutions au tableau en faisant apparaître le nombre de points pour chaque solution (explications ci-dessous) va permettre à chacun de progresser en s’appropriant progressivement de nouvelles procédures.

Sur la photo, le nombre-cible est 24. Comment fabriquer 24 avec 2 ; 5 ; 1 ; 4 et 17. C’est un tirage ouvert car riche en solutions et accessible au plus grand nombre.
17+5+2 ou 17+1+2+4 sont les solutions additives les plus accessibles.
Exemples de solutions avec plus de points en faisant intervenir d’autres opérations :
| Calcul 1 | Calcul 2 | Calcul 3 | Calcul 4 | Nombre de points |
| 2 x 4 = 8 | 17 + 8 = 25 | 25 – 1 = 24 | / | 9 points (5 + 1 + 1 + 2) |
| 2 x 5 = 10 | 17 + 10 = 27 | 4 – 1 = 3 | 27 – 3 = 24 | 11 points (5 + 1 + 1 + 2 + 2) |
| 17 – 5 = 12 | 4 / 2 = 2 | 2 x 12 = 24 | 24 / 1 = 24 | 14 points (5 + 2 + 3 + 1 + 3) |
| 17 + 1 = 18 | 5 – 2 = 3 | 18 / 3 = 6 | 6 x 4 = 24 | 18 points (Coup Mathador) |
Remarque : le système de points est simple. 5 points dès que le nombre-cible est atteint et 1 point pour chaque addition ou chaque multiplication, 2 points pour chaque soustraction et 3 points pour chaque division. Enfin, le coup Mathador rapporte 18 points (5+13), il faut utiliser les 5 nombres et les 4 opérations chacune une fois. Il est conseillé de commencer à jouer sans le système de points et d’introduire progressivement les points.


















