Le calcul mental en 6° – semaine 15

Au programme de cette première semaine de classe de l’année : du calcul mental réfléchi, avec les séries 17 et 18 et, bien sûr, le début du concours Mathador ! Une première épreuve très accessible avec une grande diversité des approches que nous allons décortiquer.

Une fin d’année centrée sur le jeu

La fin d’année 2017 a permis une consolidation des dispositifs de calcul mental axés sur le jeu. Lors des 2 dernières semaines, nous avons effectué quelques lancers de dés Mathador en prévision du concours, une séance en salle multimédia avec Calculatice et Mathador Chrono et une séance de jeux en classe. Lors de cette séance, 5 jeux sont disposés en atelier dans la classe : Trio, Mathador Flash, Détective Mathéo, Cubissimo et Polyssimo. Les trois premiers sont des jeux de calcul mental, Détective Mathéo étant une adaptation du principe de Dobble aux tables de multiplication et les deux derniers sont dans le domaine de la géométrie. Les élèves, par groupe de 4, découvrent chaque jeu en passant une dizaine de minutes par atelier.

Retours sur les échanges des dernières séries de calcul mental 17 et 18

Dans la série 17-6°  à l’oral, des échanges intéressants autour des erreurs sur les calculs de décimaux. La tentative de reproduction mentale des techniques opératoires écrites est toujours présente. Cette habitude reste difficile à déconstruire et demande du temps. Mais le message commence à passer car beaucoup d’élèves procèdent bien de gauche à droite pour calculer mentalement 24,5 + 82,8. Dans le calcul de la différence 142,8 – 42,9 , la décomposition de 42,9 en 42,8+0,1 est une aide précieuse pour atteindre 99,9. Pour permettre aux élèves de comprendre l’erreur classique 6,21 dans le calcul 3×2,7 , il est utile de rappeler que 3×2,7 , c’est aussi 2,7+2,7+2,7. Le passage par l’addition donne du sens à un calcul encore abstrait pour quelques élèves.

La série 18-6° est réalisée à l’écrit sur le petit cahier. L’écrit permet de soulager la mémoire. Mais la consigne reste de ne pas poser les opérations. Les techniques opératoires éloignent du sens du nombre, le côté algorithmique et technique l’emporte et focalise toute l’attention de l’élève. Par exemple, l’écriture en chiffre de « douze centaines, cinq dizaines et vingt-trois unité » n’est par réalisable par tous les élèves sans un passage écrit par 1200+50+23. De même pour la décomposition en somme, différence, produit et quotient de 140. C’est aussi la grande différence entre les jeux Trio et Mathador. Trio peut se pratiquer exclusivement mentalement et à l’oral alors que Mathador avec le traitement de 5 nombres et Trio avec 3 nombres nécessitent un passage par l’écrit pour de nombreux élèves. Quelques élèves commencent à développer une relation aux nombres et aux opérations où l’astuce et le plaisir prennent une plus grande place. Avec des propositions pour la décomposition de 140 comme 139+1 ; 141-1 ; 140×1 et 140:1 ou 138+2 ; 142-2 ; 70×2 et 280:2. La régularité et la répétition des situations contribuent à l’installation de cette relation. La question 5 sur la durée en minutes qui sépare 13h45 de 16h10 fait partie de la catégorie des questions vie courante. Il est important de travailler régulièrement la mentalisation de situations simples de la vie de tous les jours. Dans cette question, la réponse de 145 minutes, avec éventuellement un passage par 15+60+60+10, reste difficile pour de nombreux élèves en 6°.

Pour rappel, les deux séries 17 et 18 ne sont pas évaluées. J’indique aux élèves qu’il y a 6 questions et qu’ils pourront compter le nombre de bonnes réponses. Il s’agit d’auto-évaluation qui participe au développement de l’autonomie et de la responsabilité de chacun.

Première épreuve du concours Mathador !

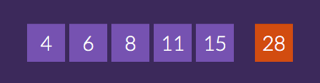
Ça y est, c’est parti pour le concours Mathador ! C’est le premier tirage pour cette semaine de rentrée. Les élèves sont prêts, les situations d’entraînement ne se compte plus et la dynamique Mathador Chrono grâce au numérique est bien en place ! Je commence par la distribution de la petite feuille pour écrire ses calculs. Je leur précise qu’ils peuvent se servir du dos de la feuille comme d’un brouillon et que dans le cadre prévu aux calculs, ils peuvent proposer plusieurs solutions. La meilleure, celle avec le plus de points, sera retenue. J’insiste sur une consigne répétée plusieurs fois déjà : commencer par chercher des calculs simples pour prendre confiance et essayer de trouver une solution simple au plus vite. Une fois cet objectif atteint, utiliser le temps restant pour chercher des décompositions plus complexes, faire intervenir la soustraction et la division ou chercher un coup Mathador. L’idée étant d’installer une démarche qui parte du simple pour aller ensuite vers une complexification des calculs. Chacun a écrit son nom sur sa feuille, je commence à écrire le tirage au tableau :

Et c’est parti pour 4 minutes de gymnastique des neurones ! La concentration est forte, pas un bruit, puis les premiers calculs sont posés sur les feuilles. Le concours 2017/2018 est lancé !

A l’issue des 4 minutes, je ramasse les feuilles. Faute de temps, il n’y aura pas de corrections en échangeant la feuille avec le voisin. Certains élèves ont pris le temps de compter leurs points et de l’écrire… de toute façon, je corrigerai et vérifierai le calculs de points !

Les premiers échanges entre les élèves laissent entendre que le tirage était facile mais personne ne pense avoir trouvé un coup Mathador. La correction est un moment intéressant pour découvrir les différents chemins et la diversité des solutions. Ce premier tirage étant très accessible et ouvert, effectivement, il y a une grande diversité des approches…

Bien que 28 soit un résultat connu dans les tables, 4×7 n’intervient pas une fois dans mes deux classes de 6°. Confirmation : la décomposition multiplicative est peu utilisée. Pourtant, avec ce tirage, on pouvait facilement fabriquer un 7 avec 15-8 puis 7×4. Le registre additif s’impose naturellement. Une large majorité des solutions commence par 15+11. La diversité des fabrications du 2 manquant pour obtenir 28, est intéressante à analyser : beaucoup de solutions en 9 points avec 6-4 ou 8-6 pour trouver 2 et obtenir 26+2=28. Quelques propositions de 8:4 pour trouver 2 puis 26+2=28, solution en 10 points. Autres propositions pour améliorer le total de points : 8-4 puis 6-4 et enfin 26+2 donne 11 points. Et la plus astucieuse, lue une fois, 8-6 puis 4:2 et 26+2. Solution en 12 points.
Quelques zéros dus à une réutilisation d’un nombre déjà utilisé. Cette analyse des différents chemins construits sur la base de 15+11 est présentée à la classe au tableau quelques jours après le tirage. Ces quelques minutes sont importantes pour permettre à chacun de découvrir des pistes nouvelles qui seront peut-être mises en application lors d’un prochain tirage. C’est à la fois un travail sur le sens des opérations mais aussi un enrichissement en procédures de calculs !