Le calcul mental en 6° – semaine 21

Nous sommes bientôt à la moitié de l’année scolaire : la régularité du travail effectué en calcul mental depuis le début de l’année commence à porter ses fruits ! La régularité et la répétition avec des situations ludiques est toujours de mise : zoom sur le jeu Calcul@kart !

Quelques retours sur les dernières séries de calcul mental, 21 et 22 

Dans la 21-6° à l’oral, les échanges autour des calculs de décimaux sont toujours riches et nécessaires. Les débats suscités par les erreurs sont très intéressants. Par exemple, 17,5+12,48 a permis d’échanger et de comprendre l’erreur classique 29,53. La numération de position a mis des siècles pour s’installer dans le monde, nos élèves peuvent légitimement avoir besoin de plusieurs mois pour la digérer ! Dans le calcul de la différence 13,5 – 3,6 que nous avons rencontré plusieurs fois sous des formes différentes, je constate moins d’erreur, la mise en place mentale progresse… Pour effectuer 1200:30, deux approches sont évoquées. L’une, que j’ai mis en indice, propose de partager la division par 30 en deux divisions successives plus simples par 10 puis par 3 en s’appuyant sur la décomposition de 30 en 10×3. L’autre méthode utilise l’opération contraire avec la technique de l’opération à trous. A savoir, combien peut-on faire de paquets de 30 pour obtenir 1200. Par tâtonnements, plusieurs élèves ont trouvé la réponse 40 par cette méthode, riche de sens des opérations. La dernière question Trio est désormais un moment très agréable en classe. L’envie et l’émulation sont fortes. Pratiquement tous les élèves trouvent des solutions inventées du nombre-cible 46 avant diffusion de la grille : 8×5+6 ; 8×6-2 ; 9×5+1 ; 7×7-3… Le mécanisme est bien en place, la consolidation des tables de multiplication avec l’effet jeu fonctionne bien !

Le fait de proposer le nombre-cible en amont est un procédé que je conseille vivement car cela incite l’élève à être créatif et à imaginer des solutions. On peut le pratiquer avec Trio et Mathador et tous les jeux avec un nombre-cible mais cela peut aussi se transférer à d’autres situations, comme inventer un énoncé de problème en donnant le nombre solution et quelques nombres à utiliser dans l’énoncé. L’élève doit alors créer le cadre dans lequel ces nombres vont opérer.

Ensuite la grille arrive sur l’écran et le jonglage, voire la jubilation, peut se mettre en place !

La série 22-6° est quant à elle réalisée à l’écrit sur le petit cahier. La question sur la décomposition d’un nombre en somme, différence, produit et quotient est désormais bien installée. Décomposer 12,8 en deux nombres en utilisant chacune des 4 opérations est une gymnastique nécessaire pour développer une aisance et une familiarité mentale avec les décimaux. Le processus est installé mais je constate une grande différence de rapidité entre les élèves. Ceux pour lesquels la construction de cette relation aux nombres et aux opérations est encore en cours ont besoin de beaucoup plus de temps qu’un élève qui a développé déjà un bon niveau de maîtrise. Encore une fois, l’importance de la régularité et de la répétition des situations est une clé dans ce type d’apprentissage. C’est un des apports majeurs mesurés par les neurosciences. 12×15 est un bon exercice mental pour expliquer la distributivité à ceux qui ne la maîtrisent pas encore. L’explication de 10 paquets de 15 que l’on ajoute ensuite à 2 paquets de 15 est bien comprise. Attention à la fausse double distributivité souvent utilisée qui consiste à proposer 110 comme réponse avec l’explication 10×10 + 2×5. Le retour aux paquets de 15 ou de 12 est une façon de convaincre que cette pseudo double distributivité est une mauvaise piste.

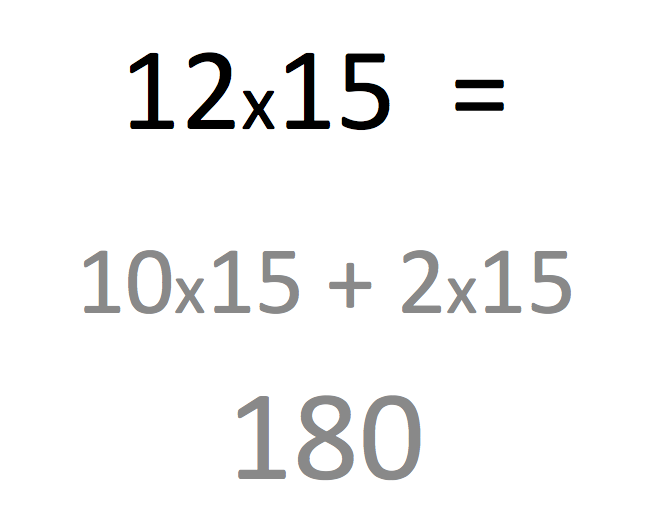
(14,4 – 3,4)x(5,5 + 4,5), le retour d’un calcul avec des parenthèses pour bien mettre en place les priorités. Les calculs intermédiaires dans les parenthèses sont assez simples, de cette façon, la surcharge cognitive n’est pas trop forte et permet la gestion mentale de la globalité du calcul avec les priorités. Enfin, la dernière question Mathador du diaporama avec 60 en nombre-cible est assez simple. Le coup Mathador est annoncé de nombreuses fois dans la classe avec (3+1)x15:(3-2). L’automatisation du divisé par 1 est en marche !

Zoom sur Calcul@kart

L’alternance entre la salle multimédia et la salle de classe se poursuit !  Toutes les deux semaines, en demi-classe nous allons une heure en salle multimédia. C’est l’occasion de faire le point du concours Mathador avec les statistiques individuelles de chaque élève, de faire un challenge Mathador Chrono et de découvrir des sites comme Mathenpoche et Calculatice. Après avoir présenté le jeu Quadricalc sur Calculatice, il y a quelques semaines, je vous propose de découvrir aujourd’hui le jeu Calcul@kart !

Le principe de Calcul@kart est très simple : le joueur pilote une voiture de course. Sur le circuit, il y a régulièrement des camions qui apparaissent sur le circuit devant la voiture et sur chaque camion est inscrit une opération.

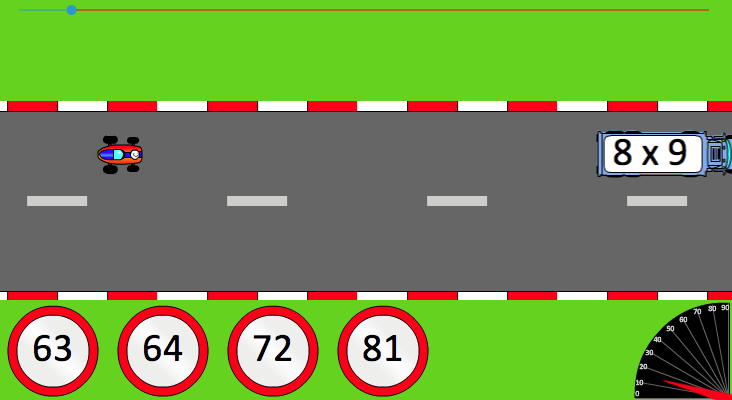
Le joueur se voit proposer 4 réponses possibles et il doit tout simplement cliquer sur la bonne réponse pour pouvoir doubler le camion.

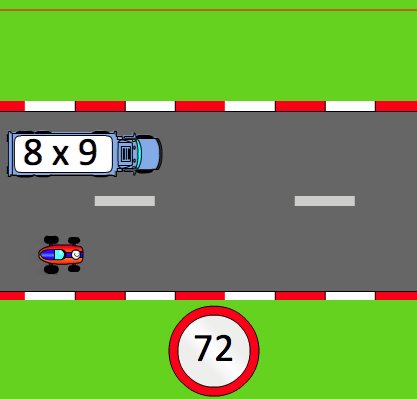
Et sinon, en cas d’erreur ou de réponse trop tardive, c’est l’accident et la voiture repart avec une vitesse au minimum. La bonne réponse est affichée pour que l’élève l’enregistre.

Le but est évidemment d’avoir le maximum de bonnes réponses pour avoir le meilleur score possible. C’est un jeu très simple qui rencontre un grand succès grâce à une façon ludique et attractive de travailler la mémorisation de résultats automatisés. Suivant le niveau choisi, les opérations sont des additions ou des multiplications et la vitesse de la voiture est modulée. Encore une fois, c’est la régularité et la répétition de ce genre d’activités qui permet de consolider des résultats dans la durée. On retrouve dans ce type de jeu un des intérêts du numérique : rendre attractif un travail de gammes qui, pratiquer de façon classique, peut devenir rapidement rébarbatif.

À dans 2 semaines !