Astuce Concours #2

Ce deuxième billet « Astuce concours » d’Eric Trouillot est l’occasion de revenir sur une épreuve du concours Mathador 16-17, d’en faire une brève analyse et de montrer aux élèves comment mieux utiliser la décomposition multiplicative dans leurs approches de calcul.

Au-delà du plaisir de chercher et de trouver, le concours Mathador est avant tout un outil qui doit permettre à l’élève de progresser dans le domaine du calcul. L’élève dispose de ses connaissances et de ses habitudes de calcul. Comme dans de nombreux autres domaines, on constate une tendance à chercher à reproduire des stratégies que l’on utilise habituellement. C’est humain, on se raccroche à ce que l’on connaît et à ce que l’on sait faire.

Utiliser le calcul à l’envers pour observer la diversité des approches.

Dans la recherche du nombre-cible, il est intéressant de constater la sous-utilisation de la décomposition multiplicative. C’est certainement une conséquence d’un apprentissage des tables de multiplication trop axé sur le sens direct. 7×9 = ? C’est l’apprentissage classique qu’il faudrait systématiquement accompagner de la pratique à l’envers, 63 c’est quoi ? La réflexion inverse fait apparaître la diversité potentielle des chemins pour fabriquer le nombre-cible.

Il est donc important de proposer d’autres chemins de calcul, d’autres éclairages. Dans cet esprit, il faut le plus souvent possible proposer à la classe un retour avec analyses et exemples du tirage de la semaine précédente. En se servant des calculs d’élèves de la classe et en montrant la diversité des approches, ce bilan régulièrement proposé doit permettre à chacun de s’enrichir grâce aux autres. Comme le concours s’étale sur plusieurs mois, il doit permettre aux élèves de pouvoir réinvestir des approches nouvelles.

Tirer le meilleur profit de la décomposition multiplicative.

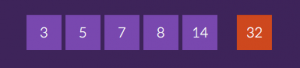
L’épreuve 6 du cycle 3 proposait un nombre-cible 32 avec les cinq nombres 3 / 5 / 7 / 8 et 14

Dans l’analyse à postériori, il est intéressant de mettre en évidence les décompositions multiplicatives de 32 : 4×8 et 2×16. Sur mes 3 classes de 6°, 4 élèves seulement utilise la décomposition 4×8 pour fabriquer 32.

Cette démarche à l’envers n’est pas naturelle, ni culturelle. Il faut vraiment insister pour développer cette pratique. D’autant plus que la décomposition des nombres est désormais au cœur des nouveaux programmes de mathématiques. Rémi Brissiaud insiste à juste titre sur l’importance de la décomposition des nombres dès le cycle 1.

Particularité de cette épreuve, l’approche 4×8 permet de trouver une solution facile et également un coup Mathador.

7 – 3 = 4 et 4×8 = 32 ; solution à 3 points

14:7 = 2 ; 5 – 3 = 2 ; 2 + 2 = 4 et 4×8 = 32 ; coup Mathador à 13 points

Pour trouver une solution rapide et facile, la plupart des élèves ont trouvé :

7×5 = 35 et 35 – 3 = 32 ; solution à 3 points

Un exemple de solution intermédiaire :

14×3 = 42 ; 8 – 5 = 3 ; 3 + 7 = 10 et 42 – 10 = 32 ; solution à 6 points