Les routines de Lionel Wanozyniak, pro du concours Mathador

Les CM1 de l’école Alice Cotteau-Blin-Péri de Leers (59) sont lauréats du concours Mathador 2021-2022 dans la catégorie cycle 3. Fin mai, l’équipe Mathador s’est entretenu avec leur enseignant, Lionel Wanozyniak : l’occasion de revenir sur sa préparation au concours et la place qu’occupent les mathématiques dans sa routine scolaire.

Quelle place prend l’exercice du calcul mental dans votre enseignement des mathématiques ?

Nous faisons une séance de calcul mental tous les jours, avec un exercice de type Mathador. Les lundi et mardi, c’est moi qui propose un tirage. Au départ, ils n’ont que le nombre cible, sans autres nombres imposés. Les élèves doivent trouver un moyen de l’atteindre avec quelques contraintes (+1, +10, dans les tables, avec une division, etc.). Après seulement je donne le tirage complet. Cela permet aux élèves en difficulté de reprendre des opérations qui ont déjà été trouvées. Chacun donne une solution : on commence toujours par les solutions les plus faciles pour aller vers le complexe. On peut ainsi montrer aux élèves qui ont une solution à 4 ou 5 points comment ils auraient pu faire pour augmenter le score.

Le tirage du mardi ressemble beaucoup, d’un point de vue opération, à celui du lundi. Ce qui permet de voir comment c’est réinvesti. En début d’année, les cibles ne dépassent pas les 40. Quand j’avais les CE1, les cibles tournaient entre dix et vingt-cinq. Avec les CM, je prends souvent des nombres cibles dans les tables et des nombres premiers. Je peux également travailler sur les doubles : avoir par exemple 36 en cible le lundi et 72 le mardi.

En période de concours, l’épreuve de la semaine est jouée le jeudi. Le vendredi, on fait également le tirage proposé sur Twitter après la récréation de 10h, ce qui permet aussi un temps de retour au calme.

Un véritable rituel a été instauré autour du calcul mental et de Mathador. Avec la classe de CE2 (n.d.l.r : elle aussi lauréate du concours), il y a une émulation. Ma collègue fait les mêmes tirages en classe et les élèves comparent leurs réponses.

Certains ont compris le fonctionnement et cherchent des calculs plus complexes, avec un nombre cible à trois chiffres par exemple. Tous les ans j’ai dans la classe un ou deux supers calculateurs et au moins la moitié de la classe me bat à Mathador en fin d’année.

Comment mettez-vous en place la phase de verbalisation  et quelles traces gardent-ils de ces moments de verbalisation ?

Nous travaillons beaucoup de choses sur ardoise, nous avons donc peu de traces écrites sur les cahiers. Il m’arrive de prendre en photo l’ardoise d’un élève pour qu’il nous explique comment il a cherché.

Quel lien avec les autres domaines mathématiques, notamment la résolution de problèmes ?

Dans la résolution de problème, la règle est de ne pas poser l’opération si on est capable de la faire de tête. En revanche, si c’est trop complexe, les élèves ont le droit à la calculatrice. La technique opératoire en problème ne m’intéresse pas beaucoup, par contre j’essaie de les forcer à utiliser le calcul mental.

En résolution de problèmes, je prends avec moi ceux qui sont en difficulté pour travailler ensemble. Les autres peuvent travailler en groupe et en autonomie. Pour tout ce qui est problème, contrairement au calcul mental, on garde une trace écrite, « une banque de problèmes ».

Comment travaillez-vous le calcul à l’endroit / calcul à l’envers ?

Le calcul mental à l’envers est proposé systématiquement : on réfléchit à comment on peut remonter petit à petit vers le tirage. Les élèves plus en difficulté partent toujours du tirage pour descendre à la cible, ils ont du mal à faire l’inverse. Ils essaient de partir de la cible en soustrayant le nombre le plus grand du tirage. Les élèves qui viennent au tableau pour expliquer leur démarche donnent beaucoup d’idées aux autres.

Comment faites-vous avec les élèves plus en difficulté ? Est-ce que l’écart se restreint en cours d’année ?

Au fil du temps, toute la classe finit par trouver un coup Mathador. C’est différent pour les élèves d’ULIS qui sont en trop grande difficulté : ils travaillent les mêmes nombres cibles, mais avec un tirage différent.

Les élèves qui ont des procédures « expertes » expliquent aux autres et, à force, certains mémorisent des calculs et faits numériques. L’entre-aide et l’émulation permettent la progression.

J’ai d’abord utilisé Mathador pour leur faire apprendre les tables. La récitation « comptine » que l’on se chante dans la tête  ne permet pas de les apprendre, alors qu’avec Mathador, s’ils veulent marquer des points, ils doivent se servir des tables de multiplication. Depuis que je joue en classe à Mathador, je ne fais plus de leçon d’apprentissage des tables, elles sont sues naturellement. Ils voient le rapport entre les tables de 2, 4 et 8, de 3, 6, 9 etc. Ceux qui ont encore un peu de mal calculent avec les doigts. Actuellement, en fin d’année, 99% des élèves connaissent leurs tables jusqu’à 10 par cœur. Pour certains, ce sont les tables jusqu’ à 15.

Ils adorent jouer avec les nombres. Chaque calculs qu’ils trouvent leur donnent envie d’en trouver d’autres. Ça ouvre de nouvelles perspectives, des nouvelles pensées : « ah oui là, j’aurais pu faire ça » etc.

Ils travaillent la logique et pas uniquement les multiplications : pour trouver des compléments à un nombre, trouver des doubles/ des moitiés. Ça marche même sur des calculs plus compliqué.

Nous avons fait il y a peu, une épreuve du concours EurékaMaths, où nous sommes aussi inscrits : on s’est rendu compte que Mathador avait beaucoup aidé. Il y a des calculs avec +99 +98, alors on fait +100 – 1 etc. on s’est rendu compte que Mathador avait beaucoup aidé. Il y a des calculs avec +99 +98, alors on fait +100 – 1, + 100 – 2, etc. Ils ont une gymnastique dans le calcul qu’ils n’avaient pas avant : ils calculent beaucoup plus vite, il y a moins d’hésitation. En début d’année, quand on proposait une opération en calcul mental, par exemple 25-17, ils posaient l’opération dans leur tête. Plus maintenant : ils décomposent et recomposent.

Vous participez depuis plusieurs années au concours Mathador : pouvez-vous nous donner des indications sur vos rituels d’avant et/ou d’après tirage ?

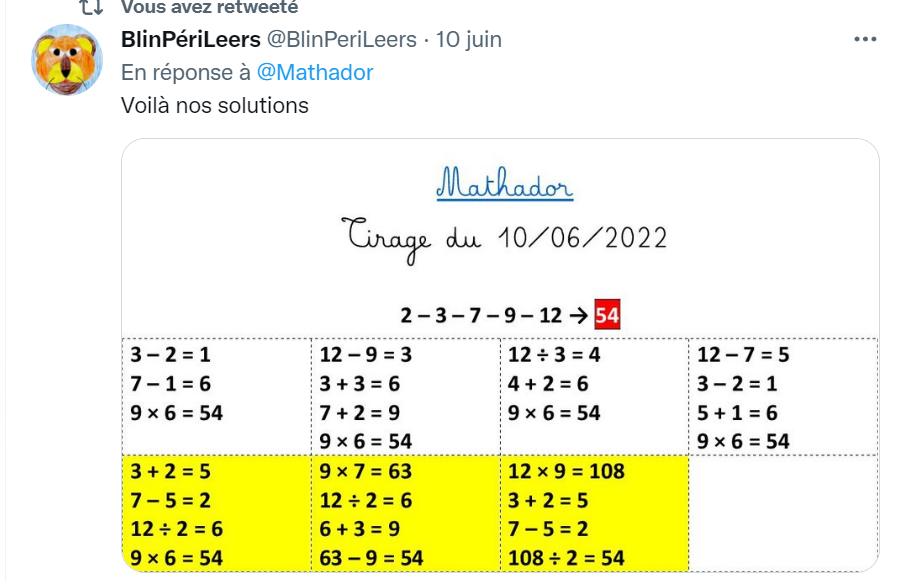
Pendant le concours, toutes les aides ont disparu. Je rassure les élèves plus en difficulté. Le « rituel » est , pendant la première minute, de chercher et écrire tous les résultats qui permettent d’arriver à la cible sans s’occuper des nombres qui ont été donnés. Puis à l’aide de ça, s’organiser pour trouver une solution d’abord facile (que l’on garde au cas où) et regarder ensuite comment on peut l’améliorer.

Après chaque tirage, on fait un temps pour expliquer quelles solutions ont été trouvées et comment on peut y arriver. Ils ont dans l’ensemble bien tous progressés.

Quel entrainement mettez-vous en place pour participer aux différents concours que vous citez ?

La programmation en maths est axée sur ce qu’on va faire tout au long de l’année avec Calcul@tice pour le calcul mental ou Eurekamaths lors de la résolution de problèmes.

On fait l’énigme EurêkaMaths tous les lundis (n.d.l.r : disponible sur Twitter). Le mardi pendant 1h on fait un rallye Calcul@tice à partir de mes archives. L’avantage, c’est qu’ils peuvent collaborer, en faisant des équipes hétérogènes : j’aime bien qu’il y ait un fort et un moins fort ensemble, car ça tire vers le haut.

Est-ce que vous utilisez, pour une pratique croisée, d’autres jeux ?

Nous avons essayé le trio une paire de fois mais ils n’ont pas trop accroché, à l’inverse des CE1 que j’avais l’année dernière. Ils ont beaucoup de jeux mathématiques dans la classe, principalement de logique. Le quarto marche bien par exemple. En jeu purement de calcul, je n’utilise que Mathador. En revanche, ils ne sont pas très Mathador sur tablette. Nous pouvons difficilement utiliser Chrono et Solo à l’école pour des raisons de connexion, mais même quand je regarde le temps de connexion hors classe, je me rends compte qu’ils ne jouent pas : certains accros vont quand même faire deux-trois parties, mais ils se connectent plus pour changer le look de leurs avatars ! Autant en classe, quand ils ont le tirage, ils sont supers contents, autant ils le sont moins si on leur propose de faire 1h de Mathador sur ordinateur. Au début ils avaient découvert la fonction tournoi, donc ils s’invitaient les uns les autres, mais ça les a vite lassés.

Avec la boite ils font des équipes deux contre deux, il y a un côté convivial, les versions numériques sont plus impersonnelles.

Comment faites-vous la liaison avec les autres collègues et niveaux, avec Mathador ?

J’ai une base de tirages que je donne à mes collègues en début d’année, qui permet de faire un tirage Mathador par semaine. Les élèves de ma collègue de CE2, que j’avais en CE1, ont réclamé Mathador. C’est pourquoi nous faisons un tirage commun, cela permet que les CE1 viennent parfois montrer leurs solutions à mes CM1. Avant les vacances, on fait un après-midi jeux mathématiques collectif.

Nous avons dans l’école une classe double niveau « CP/CE1 » qui pratique aussi Mathador. De fait, les CP sont là quand les élèves de CE1 font le mathador. Pour les CP, le tirage est adapté : on ne garde que 3 dés, addition et soustraction seulement, etc. Les multiplications arrivent naturellement quand les élèves voient les limites de l’addition : ils deviennent demandeur de la multiplication.

Quand j’avais les CE1, tant que l’on n’avait pas vu la multiplication, la solution des tirages que je faisais pouvait se trouver uniquement avec des plus et des moins. Le jeu amenait les apprentissages, ça partait d’un besoin de l’enfant qui avait besoin de telle opération pour y arriver. Pour les élèves, ça n’est que du jeu à chaque fois. Derrière, on voit que les tables sont sues, l’agilité en calcul est plus précise…

Comment faites-vous le lien entre maths et réalité, maths et quotidien ?

On a construit un arbre de Pythagore : il a fallu calculer les segments. Idem pour la spirale de Fibonacci où on réfléchit au rapport entre les nombres. De toute façon, ils ont besoin de manipuler, quand c’est trop abstrait, ils perdent vite le fil. Dans les défis EurêkaMaths, certains ont besoin de manipuler, d’aller chercher des objets, notamment des cubes pour refaire des assemblages.

La manipulation reste encore possible pour ceux qui en ont besoin. Hormis pour le concours, s’ils ont besoin de leur règle de Pythagore pour leur calcul, c’est autorisé. On essaie d’abord de faire sans… mais je préfère qu’ils utilisent la règle plutôt qu’ils mémorisent un mauvais résultat.

Lors de l’apprentissage des tables, ils passent d’un calcul réfléchi à un calcul automatisé. Ils sont plus à l’aise avec les nombres et ont compris le sens de la multiplication. Ça devient plus facile pour eux lorsqu’on aborde la division.

Lors de l’apprentissage des tables, ils passent d’un calcul réfléchi à un calcul automatisé. Ils sont plus à l’aise avec les nombres et ont compris le sens de la multiplication. Ça devient plus facile pour eux lorsqu’on aborde la division.

Quels conseils donneriez-vous aux autres participants ?

Prendre du plaisir est le plus important ; regarder ce que l’on a fait, est ce que l’on s’est amélioré. Ils notent tous les résultats, ils font un graphique pour voir leur évolution. Le premier conseil pour Mathador c’est prendre du plaisir. Les élèves ne disent pas « on fait du Mathador » mais « on joue au Mathador » pour eux ça n’est même pas une discipline scolaire, juste un jeu. Pour le plus petits on cherche à avoir une meilleure solution, pas forcément une meilleure que celle du voisin mais une meilleure que celle qu’on a trouvé avant. Je fais attention aux élèves très prétentieux qui peuvent avoir tendance à chercher la comparaison et bloquer les camarades. Les autres sont en revanche capables d’aller vers les élèves plus en difficulté et leur expliquer la démarche. Quand on fait des après-midi jeux j’aime bien qu’il y ait un fort et un moins fort ensemble car ça le tire vers le haut. Pareil pour le rallye calcul@tice.

Un grand merci à Mr Wanozyniak pour sa disponibilité!

Vous pouvez suivre les cm1 de l’école Alice-Cotteau-Blin Peri sur twitter.