Le calcul mental en 6° – semaine 13

Le processus de mentalisation de la relation aux nombres et aux opérations est maintenant en cours. Il donne déjà des résultats pour les élèves qui avaient déjà de bonnes bases. Pour les autres, la fréquentation de cet univers dans la durée permettra à chacun de construire son propre puzzle mental.

Quelques retours sur les dernières séries de calcul mental

Les séries 15 et 16 ont encore donné l’occasion d’échanger autour des différentes méthodes en calcul mental réfléchi. La série 15-6° à l’oral permet des échanges intéressants autour des erreurs et des difficultés à effectuer mentalement la différence entre deux décimaux, 21,5 – 6,7. La tentation de reproduire mentalement les techniques opératoires est toujours grande. Cette habitude est difficile à déconstruire. Il faut toujours insister sur la décomposition des nombres en plusieurs nombres pour faciliter ensuite la soustraction. Ici 21,5 – 6 – 0,5 – 0,2 ou 21,5 – 0,5 – 6 – 0,2 est une aide pour certains élèves mais devra être mis en application de nombreuses fois. 15,4×10 donne l’occasion d’expliquer que le « on décale la virgule d’un cran à droite » n’a pas beaucoup de sens, c’est un « truc » alors que dire « chaque chiffre se décale d’un cran à gauche et la virgule ne bouge pas » a plus de sens car, comme on multiplie un nombre par 10, le chiffre des unités devient chiffre des dizaines, le chiffre des dizaines devient chiffre des centaines et le chiffre des dixièmes devient chiffre des unités. 72:6 est encore l’occasion de leur déconseiller de poser l’opération dans leur tête mais plutôt de procéder à l’envers avec la table du 6, en partant par exemple de 60 = 10×6. Cette idée est proposée par plusieurs élèves. La gymnastique Trio est désormais bien en place, la plupart des élèves trouvent après 1 ou 2 minutes une solution sur la grille vidéo-projetée. Il est très intéressant de faire entourer chaque solution Trio sur le TBI par les élèves de façon à bien visualiser l’ensemble de toutes les solutions.

Dans la série 16-6°, à l’écrit sur le petit cahier, la question sur la décomposition d’un nombre est généralisée aux quatre opérations. La mécanique à l’envers commence à bien être en place, les exemples de décompositions sont riches et divers. Dans la question 3, pour apporter une aide pour effectuer 25:10, l’idée d’imaginer un partage de 25€ en 10 personnes facilitent le passage d’entiers à décimaux qui restent un cap difficile à franchir pour de nombreux élèves en 6°. Ils acceptent facilement l’idée que la réponse est supérieure à 2€ et inférieure à 3€, la suite est encore à construire pour certains. La répétition des situations dans la régularité est encore une réponse pour laisser ce temps nécessaire à certains élèves. Enfin, pour mettre en lien la pratique régulière du calcul mental et le sens des opérations, des problèmes très courts de vie courante vont permettre de tisser ces liens et de les entretenir avec le temps. C’est l’objectif du petit problème de la question 6. L’opération attendue 60 – 2,5 est bien trouvée par la plupart des élèves mais la réponse 58,5 au lieu de 57,5 est encore proposée par quelques élèves. Il y a encore du travail pour mentaliser les nombres et les opérations !

Une seconde évaluation de calcul mental 

Les vacances de Noël se profilent  à l’horizon, c’est le moment de mesurer pour la deuxième fois, depuis la rentrée, les acquis en calcul mental ! Une évaluation Eval2-112017 de 10 questions abordées dans les semaines précédentes est donc proposée. Les résultats sont satisfaisants pour la très grande majorité. Ils participent à la consolidation de cette construction de la relation aux nombres et aux opérations dans un climat de confiance, facteur important de la réussite. Les élèves sont demandeurs de tests chiffrés. Il ne faut pas en abuser pour garder l’envie et le plaisir des apprentissages, mais quelques retours réguliers sont nécessaires pour mesurer les évolutions. Il faut aussi installer l’autoévaluation permanente. Les diaporamas le permettent avec un comptage personnel des bonnes réponses.

Préparation du concours Mathador !

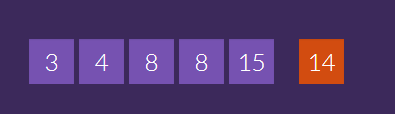
Le concours Mathador débutera en janvier. D’ici là, nous sommes dans la période d’entrainement ! Ces entraînements peuvent prendre différentes formes. Par exemple, la dernière question du diaporama 16 propose 57 avec 4/6/2/10/9. Nombreux sont ceux qui passe par 6×10 puis ensuite fabrique 3 avec 9 – 4 – 2 pour finir par 60 – 3. Les coups Mathador sont de plus en plus nombreux avec ici 6×9 + (10 – 4):2

Des tirages d’entrainement sont proposés chaque semaine sur la plate-forme internet du concours.

Chaque enseignant inscrit au concours est libre de les utiliser ou non. J’ai prévu d’en faire un ou deux dans les conditions réelles du concours. C’est-à-dire, avec la présence d’une petite feuille sur laquelle chaque élève doit écrire sa solution sous la forme d’opérations écrites en ligne. C’est l’occasion de pratiquer la correction collective. A l’issue des 4 minutes de recherche, les élèves échangent leur feuille avec un voisin qui effectue la correction et le comptage des points. Le professeur peut ensuite ramasser et vérifier les totaux.

Autre possibilité, lorsque l’occasion se présente : il reste 10 minutes à la fin d’une heure car l’activité en cours se termine un peu plus rapidement que prévu. On lance les dés, un dé par élève, les nombres notés au tableau, puis recherche quelques minutes sur le petit cahier. Ensuite différentes solutions sont écrites au tableau par les élèves. On essaye de proposer parmi les solutions annoncées, une progression dans les points avec éventuellement un coup Mathador. Le lancer de dés est un peu ma variable d’ajustement de fin d’heure !

Depuis un peu plus d’un mois les élèves ont leurs identifiants Mathador et jouent, pour certains, régulièrement à Mathador Chrono et Solo. Je suis l’évolution des statistiques de classe de mon compte Mathador Classe. Les parties en réseau se multiplient et participent à la création d’une dynamique de classe. Les élèves comparent leurs scores, font des parties à plusieurs, chez eux ou au CDI où ils échangent des conseils sur le choix de nombres et d’opérations. L’addition des diaporamas, des séances de calcul mental par le jeu en classe, en salle multimédia commence à opérer. L’alchimie se met en place, il faudra l’entretenir tout au long de l’année. La mentalisation de la relation aux nombres et aux opérations est en marche !

Rendez-vous en janvier pour les premières épreuves du concours et d’ici là, je vous souhaite de très bonnes vacances et de joyeuses fêtes  !