Exercices de calcul mental gratuits et sans outils
Les supports pour pratiquer le calcul mental direct sont nombreux. Le jeu bien sûr, le numérique aussi. On peut aussi faire du calcul mental sans support particulier à la frontière du jeu.

La chaîne d’opérations que je présente ci-dessous est très ancienne. Au début des années 2000, lors de la finale du championnat de calcul mental par classe de mon collège, le Principal était venu, les élèves étaient très fiers. La finale, avec évidemment deux très bons groupes, était intense. Egalité parfaite, 17 partout à l’issue de l’épreuve. Pas de prolongations, ni de penaltys mais le Principal me suggère une idée dont il se souvenait lorsqu’il était à l’école primaire… Il a inventé une chaîne d’opérations qui a permis de départager les deux équipes !
La chaîne d’opérations

Le principe est très simple. Il suffit d’annoncer un nombre de départ à toute la classe puis d’enchaîner quelques opérations annoncées les unes après les autres en laissant un temps de réflexion entre chaque.
Tout se passe mentalement, on ne donne pas les résultats intermédiaires et chaque opération annoncée s’applique au résultat trouvé précédemment. A la suite de la dernière opération, il suffit de demander à un volontaire d’annoncer le résultat final qu’il a trouvé. En cas d’erreur, on demande à un autre volontaire. La bonne réponse annoncée, on reprend la chaîne depuis le début en donnant toutes les réponses intermédiaires, éventuellement par l’élève qui a trouvé. La chaîne d’opérations peut se pratiquer à tous les niveaux, il suffit d’adapter le choix des nombres et la difficulté des opérations à la classe.
Quelques exemples :
| Cycle 2 | Cycle 3 | Cycle 4 | Lycée |
| 12 | 47 | 7,5 | 3 |
| +5 | +5 | +4,5 | Puissance 4 |
| -10 | -40 | x100 | Racine carrée |
| x2 | +18 | -450 | x13 |
| +16 | x3 | ÷3 | ÷3 |
| La moitié | ÷2 | -100,1 | -50 |
Le quinze vainc (sur une idée originale de Martin Gardner)

C’est un jeu pour deux très simple à fabriquer. On peut aussi jouer sur une feuille avec chacun un stylo.
Le jeu est simple et rapide. Il s’adresse à tous dès le cycle 2. Si l’on fait plusieurs parties à la suite, il faut alterner le joueur qui commence. Il faut 9 jetons avec 1, 2, 3, 4, 5, 6, 7, 8 et 9 écrits dessus ou écrire les 9 chiffres sur une feuille de papier.
A tour de rôle, chacun choisit un jeton ou écrit un des 9 chiffres. Ce chiffe n’est alors plus disponible : le jeton a été utilisé ou le chiffre a été rayé sur la feuille. Le premier des deux joueurs qui arrivent à fabriquer une somme de 15 avec 3 nombres à gagner.
Il s’agit d’un jeu de décomposition dans lequel il y a de la stratégie car il faut surveiller la somme de son adversaire et l’empêcher de fabriquer 15 avant soi ce qui va modifier mon raisonnement initial.
On peut faire un lien avec les carrés magiques 3×3 dont la somme magique est 15 et correspond à la somme de trois nombres alignés dans le carré magique. Il y a fort à parier que Martin Gardner devait avoir un carré magique dans un petit coin de sa tête lorsqu’il a eu l’idée du Quinze Vainc. On retrouve aussi ce principe de somme 15 avec trois nombres dans le jeu de société Triolet.
Le jeu de la table : pour réviser les tables de multiplication
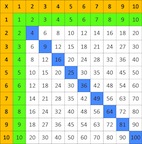
C’est un jeu pour deux ou plus, simple à fabriquer. Il s’agit d’un jeu d’entrainement de connaissance des tables de multiplication. Il suffit de reproduire un tableau à double entrée avec 10 lignes et 10 colonnes numérotées de 1 à 10 en ligne et en colonne.
Le but est de remplir les cases de ce tableau avec les résultats des tables de multiplication.
L’idéal est de disposer de 2 dés à 10 faces de deux couleurs différentes, l’un correspond aux lignes et l’autre aux colonnes. A tour de rôle, chacun lance les 2 dés et doit trouver le produit des deux nombres obtenus par les deux dés. Si on ne possède pas deux dés à 10 faces, on peut les remplacer par des cartes à jouer, par exemple de 1 à 10 cartes noires pour les lignes et de 1 à 10 rouges pour les colonnes. On peut fixer un délai maxi pour donner la réponse. La réponse doit être validée par l’ensemble des joueurs et ensuite inscrite dans le tableau. Chaque joueur choisit un stylo d’une couleur. Le gagnant est celui qui a le plus de réponses de sa couleur.
On peut très bien imaginer une adaptation pour les plus jeunes avec les tables d’addition exactement sur le même principe de jeu.
L’épreuve par 9

C’est un jeu pour deux dans le registre de Mastermind®, sauf qu’ici il faut trouver un nombre caché. Un des deux joueurs choisit un nombre entier entre 1 et 100, le note sur une feuille sans le montrer à l’adversaire. L’autre joueur a pour objectif de trouver ce nombre.
Pour ce faire, il écrit les neuf premiers nombres entiers sur une feuille : 1, 2, 3, 4, 5, 6, 7, 8 et 9. Il en choisit deux dans la liste, les raye, et fait l’opération de son choix avec et annonce le résultat.
- Celui qui a caché le nombre doit annoncer si le résultat est plus petit ou plus grand.
- Celui qui cherche peut alors choisir un nombre non rayé de sa liste et le combiner avec le résultat annoncé précédemment en faisant une nouvelle opération de son choix et ainsi de suite jusqu’à trouver ce nombre caché. S’il n’a pas trouvé avant d’avoir rayé les neuf nombres de sa liste, il réécrit une nouvelle liste 1, 2, 3, 4, 5, 6, 7, 8 et 9 et continue. Le but est de trouver en rayant le moins possible de nombres.
Une fois trouvé, on échange les rôles.
La grille de nombre croisés

La grille de nombres croisés est l’équivalent dans l’univers des chiffres des grilles de mots croisés pour les lettres. C’est un exercice solitaire qui est donc à la limite du jeu, au sens jeu à plusieurs. Mais cela reste une très bonne gymnastique mentale avec des nombres.
Principe du jeu
Des définitions horizontales et verticales permettent de placer un chiffre par case. Les nombres s’entrecroisent et forment au final une grille complète qui doit vérifier toutes les définitions. Dans ces dernières, on retrouve des calculs mais aussi de la numération, du vocabulaire spécifique faisant référence aux différentes familles de nombres, aux propriétés des nombres, aux propriétés des opérations. Comme pour les grilles de mots croisés, il y a des niveaux de difficultés qui peuvent aller de très facile à expert.