Primaire – collège : regards croisés sur l’enseignement des mathématiques
Début février, Éric Trouillot et Cristine Géobard, enseignante à Millay dans la Nièvre, ont échangé à propos de leur pratique des mathématiques avec leurs élèves : en CM1-CM2 pour Cristine, au collège pour Éric. L’occasion d’aborder leurs expériences, leurs points de vue sur l’enseignement du calcul et la liaison entre l’école et le collège.
Comment travaillez-vous la décomposition des nombres ?
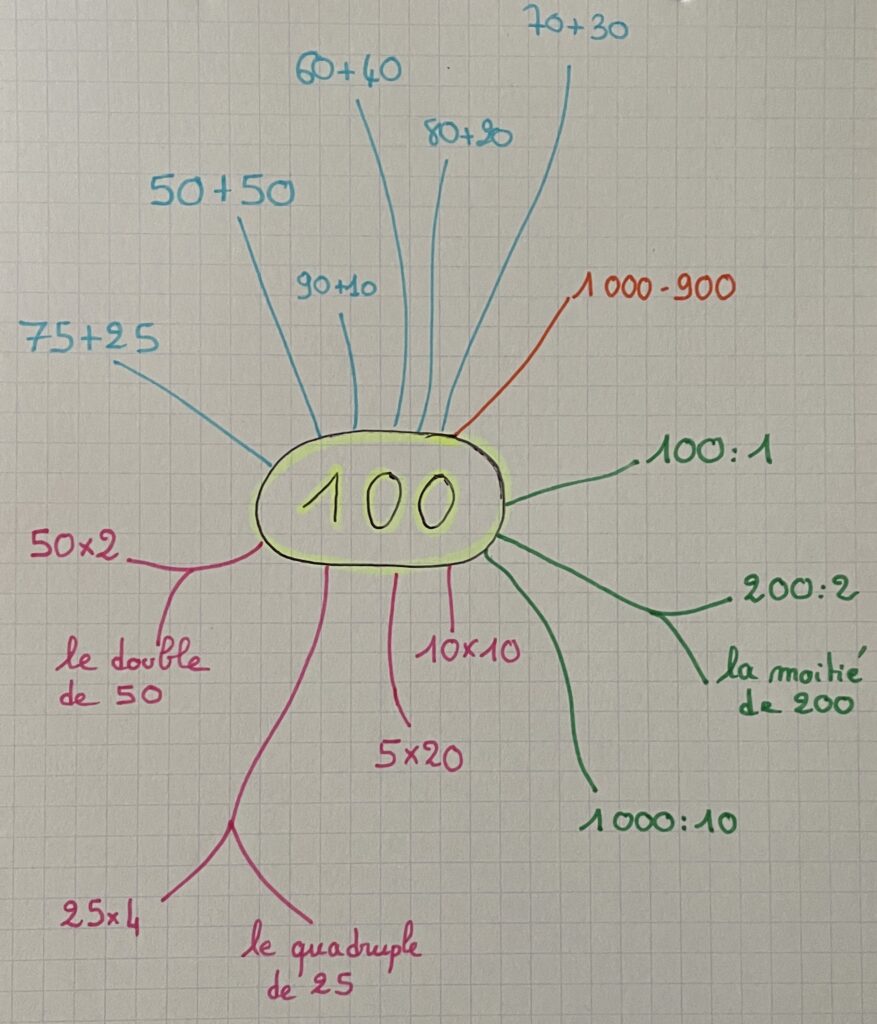
C.Géobard : La décomposition est une tâche incontournable pour une bonne construction du nombre, qui permet une utilisation plus aisée dans les autres domaines. Il faut un enseignement explicite de cette composition/décomposition. On la fait avec des activités ritualisées, la construction de famille de nombres, la résolution de problèmes numériques ou de mesure… Elle est à mettre en lien avec le calcul, où l’on va plutôt construire les tables de calculs, des cartes mentales sur les nombres 100, 50… Ce travail de décomposition s’accompagne d’une verbalisation avec l’utilisation du vocabulaire mathématique en situation qui permet de construire le sens : par exemple « moitié » c’est « divisé par deux », « + 100 » c’est « ajouter une centaine ». Et il est nécessaire de garder une trace écrite construite collectivement pour enrichir le répertoire de la décomposition.
E.Trouillot : La décomposition est travaillée avec des diaporamas présentant des situations de jeu, notamment Trio et Mathador, et des situations plus classiques : on donne un nombre, les élèves décomposent sous forme de sommes, de quotient, de multiple. Cela créé un répertoire mental, et du lien entre les nombres et les 4 opérations. Ces liens se fabriquent petit à petit. L’idée de la décomposition n’est pas naturelle, on a l’habitude du calcul mental classique, à l’endroit : en s’entrainant le plus tôt possible et régulièrement à décomposer, à travailler à l’envers, on fait des familles de nombres qui s’organisent mentalement. En décomposant, on apprend à composer, on progresse en calcul mental classique.
CG : L’apprentissage des tables change : la mémorisation des tables se fait par la construction et la manipulation de celles-ci. On se pose la question du lien entre les nombres, on utilise ses acquis pour reconstruire ce que l’on n’a pas encore mémorisé : par exemple 2 x 4, c’est 2 x 2 x 2, c’est 4 + 4, c’est « le double de 4 » ou le « quadruple de 2. On peut aussi employer les calculs à trou : 6 x quelque chose est égal à 42. Le lien se fait plus facilement. On voit des résultats qui reviennent qui se font de différentes façons (9 x 4 ou 6 x 6 ou 9 x 2 x 2…).
ET : Et les tables se mettent en place naturellement.
CG : Connaitre ses tables de multiplication par cœur peut freiner les élèves en Mathador et Trio car ils ne vont pas manipuler la cible en la décomposant pour envisager les calculs possibles mais ils vont chercher, par des opérations successives à l’atteindre. On ne travaille sans doute pas assez la décomposition dès la maternelle (avec du matériel type réglettes, Numicons…).
ET : Ça a cependant commencé à changer grâce à Rémi Brissiaud, qui a permis une prise de conscience à ce sujet, mais ça sera long, car dans les familles, la société, il y a une représentation à l’ancienne du calcul mental. C’est comme une récitation, dénuée de sens. Or i Il faut donner du sens à ce qu’on dit : les nombres sont abstraits, la décomposition met du lien là où il y en n’a pas. On peut ouvrir grâce à Mathador mais c’est une habitude culturelle et on a besoin d’acclimatation, de développer la culture du « à l’envers ». On ressent une différence entre ceux qui ont pratiqué Mathador avant le collège et ceux qui commence plus tard. Cela influence jusque dans la résolution des problèmes, certains ne posent même plus les opérations.
CG : Pour la résolution de problèmes, on peut trouver encore la culture : « pour résoudre il faut une opération posée et une phrase réponse ».
ET : De moins en moins aujourd’hui ! Il faudrait que les élèves posent les opérations si ils en éprouvent le besoin, et pas par principe. On pourrait définir 3 stades de calcul : mental au départ, écrit et posé si le besoin se fait sentir, et si c’est compliqué, instrumenté avec la calculatrice, l’ordinateur, le Smartphone…
À l’école de Millay, vous semblez aborder les mathématiques avec beaucoup de manipulation, voire de création, qu’est-ce que ça permet de travailler dans l’apprentissage des mathématiques ?
CG : Le travail d’équipe sur les différents cycles permet d’avoir une vision plus globale sur la résolution de problèmes mathématiques. Manipuler c’est rattacher les mathématiques au réel. La manipulation est une première étape dans le parcours de résolution de problèmes, quand l’élève s’en détache, il accède à l’abstraction. La manipulation est un levier pour les élèves moins à l’aise.
ET : Au collège on manipule moins, pour des raisons pratique liée à l’emploi du temps : pas simple sur une heure. On devrait pourtant pouvoir manipuler tout le temps : un enfant a besoin de mettre du lien avec un objet, c’est important. Cela fait partie du « Plan Maths1 » : manipuler, verbaliser, abstraire. En classe, j’ai quelque casse-tête, tangram. Mais manipuler ce n’est pas que le tactile, c’est aussi une manipulation mentale avec le tâtonnement, la recherche. On peut faire le lien vers l’abstrait grâce à la verbalisation. L’élève doit pouvoir mettre des mots sur ce qu’il fait pour qu’on puisse lui dire si c’est juste, et on peut le faire collectivement.
CG : Une phase de verbalisation collective est importante, tout comme les écrits réflexifs. Car ce sont les traces de la démarche des élèves, des fenêtres sur la pensée, le cheminement, les stratégies des élèves. Ces traces sont réutilisées au moment de la verbalisation collective, elles vont être validées, invalidées, permettre la remédiation. Même si l’écrit est imparfait, parce qu’orthographe approximative, syntaxe fragile, présence de dessins, schémas…, ce n’est pas grave. Il nous donne à voir l’état de la pensée à ce moment-là et permet de proposer une réponse adaptée à chacun. La verbalisation enrichit le répertoire numérique des plus fragiles, développent les automatismes. Pendant la phase de verbalisation, je fais commencer les élèves en inclusion, ce qui leur permet de proposer une solution et d’acquérir de l’estime de soi. La verbalisation est un incontournable de l’apprentissage et un outil de confiance en soi.
Les mathématiques peuvent sembler assez abstraites, comment les rendre concrètes pour les élèves, leur donner du sens ?
ET : Il faut verbaliser et manipuler ! En donnant du sens, les maths suscitent des émotions. On a une idée trop « carrée » des maths, stressante et anxiogène. Avec le jeu, on change l’image négative des maths. Les émotions sont positives et collectives. On suscite l’envie et le plaisir. Au collège, le changement de classe chaque heure est un frein à l’installation d’une culture ludique avec plus de manipulation. Et pourtant, ce besoin de manipulation, notamment chez les 6 e – 5e, est très fort.
CG : Donner du sens c’est faire du concret : dans notre école, on part au jardin faire des mesures du potager par exemple, pour rendre moins abstrait, pour inscrire les maths dans le réel (On essaye de mettre en pratique ce qu’on a appris en classe : on prend des objets de mesure, le double décimètre par exemple, et on se rend compte que ça ne marche pas. On découvre alors d’autres objets de mesure et on répond à la question « à quoi ça me sert dans la vie courante ? ».
Comment travaille-t-on le calcul mental au collège et au primaire : quels points communs ou différences retrouve-t-on au moment du changement de niveau ? Y a-t-il possibilité de travailler ensemble, et si oui avec quels outils de classe, pour que la transition se fasse en douceur ?
CG : Les échanges inter-degrés autour du Mathador marchent bien : avec une collègue de collège, on planifie un temps Mathador, chaque classe cherche de son côté, à la fin tout le monde partage les résultats. Les classes se voient aussi physiquement une après -midi.
ET : C’est simple à mettre en place pour une liaison école-collège.
CG : Et c’est un excellent moteur dans la liaison école-famille aussi. Nous avons par exemple organisé une soirée Mathador parents/enfant.
ET : Avec Mathador, le système des points permet d’adapter le niveau. Un même tirage peut être proposé aux 6e et aux 3e. Il faut un tirage ouvert : c’est-à-dire un tirage dans lequel il y a des solutions faciles, moyennes et difficiles.
CG : On peut aussi travailler avec un projet géométrique : on travaille sur le même thème avec d’autres classes et on élabore une œuvre collective. La liaison école – collège se fait toujours à travers des projets : de jeux, de géométrie. Cela permet de dépasser la notion pure, on passe au pourquoi on étudie ça, comment on grandit avec ça.

Avez-vous des conseils pour accompagner les élèves en difficultés (stress, élèves dys…) et leur redonner confiance en eux ? Pour « dédramatiser » la pratique des mathématiques, du calcul mental ?
ET : Avoir recours au jeu permet de dédramatiser. L’enfant oublie le cadre anxiogène, il y a de l’aléatoire, on tâtonne et c’est moins scolaire. C’est très important de sortir du cadre et d’essayer. La considération du jeu entant qu’outil pédagogique avance vraiment. Il y a eu des débats il y a 20 ans, maintenant on se rapproche de nos voisins belges et suisses qui ont déjà cette culture. Le numérique aussi est une piste quand on peut, car il permet de se tromper et personne, sauf l’ordinateur, ne le sait. L’élève peut tester, tâtonner et enclencher quelque chose de positif.
CG : Le jeu ne leur donne plus l’impression d’être dans quelque chose de scolaire. Il faut aussi que nous, les enseignants, soyons plus clairs dans le « contrat didactique », ce qu’on attend d’eux : c’est-à-dire que l’on n’attend pas qu’une seule réponse, qu’une seule démarche : celle donnée par la maitresse et c’est tout. Il faut être plus explicite dans ce que l’on attend et ne plus les laisser s’enfermer, les autoriser à se tromper, à chercher, à suivre une démarche différente de celle des autres etc. Le numérique permet ça, comme avec le Défi table ou Mathador avec une avancée par pallier de difficulté.
ET : Ça permet également de faire le lien école-maison. On peut voir le progrès de certains élèves grâce au numérique et certains arrivent à dépasser le maître (automatisme, vitesse). Quelques limites cependant : certains passent beaucoup de temps sur Calcul@TICE ou Mathador par exemple, c’est très positif pour la fabrication du répertoire mental grâce à ce travail de gammes mais cela peut creuser encore davantage les écarts.
CG : Il peut aussi y avoir un blocage de la part des familles par rapport au numérique. Le numérique est intéressant quand on peut avoir un retour sur ce qu’ils utilisent : le temps passé, les signes opératoires, etc., et que même à distance on peut suivre la progression des élèves.
ET : Le numérique est aussi un facilitateur de travail répétitif : il développe l’aisance mentale qu’on peut comparer à des pratiques en musique ou en sport, avec l’indispensable travail de gammes !
[1] Plan pour l’apprentissage des mathématiques, porté par C.Villani et C. Torossian en 2018
Vous pouvez suivre l’école de Millay sur Twitter


















