Calcul mental en classe : exemple de diaporamas et d’utilisation du numérique

Je l’avais développé dans mon dernier billet du blog sur le calcul mental en classe. Le diaporama est un outil idéal pour faire vivre la régularité du calcul mental, en l’intégrant dans une progression annuelle de calcul mental.

Le diaporama s’adresse à la fois à la mémoire visuelle avec l’affichage sur l’écran ou le TBI, et à la mémoire auditive avec la verbalisation et les échanges dans la classe. Ce croisement favorise la mémorisation qui suit la compréhension.

Le principe du diaporama est également en phase avec les préconisations majeures des neurosciences cognitives :

• Attention
• Engagement actif
• Régularité-répétition
• Retour d’information rapide

Le feedback, souligné comme important par les neurosciences, est un point fort du diaporama. L’élève cherche et obtient un retour immédiat sur la validation ou non de sa recherche. C’est peut-être une des raisons pour lesquelles la grande majorité des élèves adhèrent au calcul mental et au plaisir qu’il procure. Il s’agit peut-être, tout simplement d’une forme d’exercice intellectuel en phase avec le fonctionnement de notre cerveau.

En lien direct avec la didactique du calcul mental, le diaporama permet d’intégrer des situations de calcul automatisé et des situations de calcul réfléchi. Le temps de recherche et la diversité des échanges deviennent alors variables.

Dans le triptyque R-R-V (Régularité-Répétition-Verbalisation) que j’évoque souvent à propos de la mise en place du calcul mental dans la classe, c’est sur le V de verbalisation que je vous propose de revenir dans ce billet. Cette étape est fondamentale dans la phase de compréhension pour accéder au sens, puis à la mémorisation. Les atouts pédagogiques sont multiples :

• Ils permettent à chacun de s’approprier des mécanismes et des raisonnements ne faisant pas encore partie de son propre répertoire.
• Ils laissent une place à l’erreur qu’il faut traiter normalement comme une étape naturelle du processus d’apprentissage.

Les fichiers calcul, heureusement en diminution, mais qui étaient très en vogue il y a peu encore, n’ont pas aidé à installer cette culture de la verbalisation. La gestion de classe avec des effectifs élevés est également un frein important, sans oublier les collègues qui ne sont pas encore équipés d’un ordinateur et d’un vidéo-projecteur, évidemment indispensables.

Exemples d’échanges en classe de 6° lors de diaporamas 

Au cœur des échanges, on retrouve le calcul mental réfléchi, comme par exemple 4321+ 999 dans le diaporama 8. C’est une bonne illustration de l’apport du mental sur l’écrit. L’élève qui cherche à reproduire les techniques opératoires écrites se rend compte très vite qu’il existe une meilleure solution. Un camarade de la classe explique qu’il suffit d’ajouter 1000 puis de soustraire 1. Un autre expliquera qu’il a « pris » le 1 de 4321 pour l’ajouter à 999 et fabriquer 1000 de façon à ensuite l’ajouter à 5320.

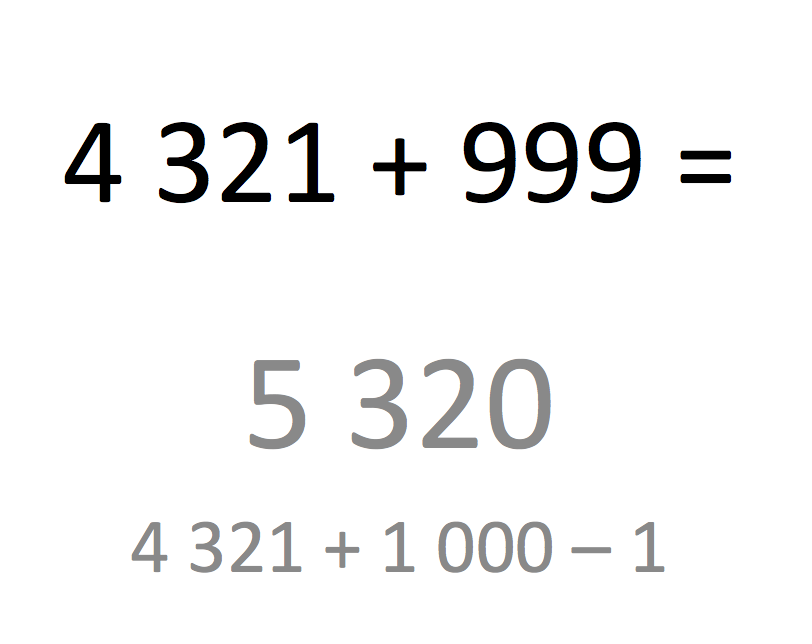Ces échanges, vécus dans la classe sont une vraie richesse pédagogique. Il valide que, dans ce genre de situation, il est possible d’apprendre par l’écoute des autres. Dans le diaporama 10, l’exemple 4 x 17 x 25 est plus difficile. J’annonce qu’il y a une astuce à trouver pour faciliter le calcul. L’explication à toute la classe par un élève que l’on peut faire 4 × 25 d’abord puis 17 ×1 00 ensuite est très intéressante. Cet exemple fait suite à un 5 x 23 x 2 la semaine précédente. L’associativité de la multiplication est bien comprise par certains et encore en construction pour d’autres, une preuve supplémentaire que répétition et régularité sont deux piliers dans l’enseignement du calcul mental.

Au programme du diaporama 7, on retrouve toujours un peu de calcul mental automatisé comme par exemple 12 × 10 et 70 : 10. Il s’agit d’une bonne occasion pour redemander à un élève la règle qui s’applique et de lui donner du sens en revenant à la définition de la multiplication et de la division.

On retrouve un 72 × 100 et un 1500 : 100 dans le diaporama 9. Une semaine entre les deux diaporamas permet de réactiver la règle en insistant sur son extension. 

Dans la série 15 , on retrouve des échanges intéressants autour des erreurs et des difficultés à effectuer mentalement la différence entre deux décimaux : 21,5 – 6,7. La tentation de reproduire mentalement les techniques opératoires est toujours grande. Cette habitude est difficile à déconstruire. Il faut toujours insister sur la décomposition des nombres en plusieurs nombres pour faciliter ensuite la soustraction. Ici 21,5 – 6 – 0,5 – 0,2 ou 21,5 – 0,5 – 6 – 0,2 est une aide pour certains élèves, mais devra être mis en application de nombreuses fois. 15,4 × 10 donne l’occasion d’expliquer que le « on décale la virgule d’un cran à droite » n’a pas beaucoup de sens, c’est un « truc », alors que dire « chaque chiffre est décalé d’un cran vers la gauche et la virgule ne bouge pas » a plus de sens. Lorsqu’on multiplie un nombre par 10, le chiffre des unités devient chiffre des dizaines, le chiffre des dizaines devient chiffre des centaines et le chiffre des dixièmes devient chiffre des unités. 72 : 6 est encore l’occasion de leur déconseiller de poser l’opération dans leur tête, mais plutôt de procéder à l’envers avec la table du 6 en tâtonnant ou en partant de 60 = 10 × 6 puis de compléter. Cette idée est d’ailleurs proposée par plusieurs élèves.

Dans la série 17, la tentation de reproduction mentale des techniques opératoires écrites reste forte, et encore formulée à l’oral. Cette habitude reste difficile à déconstruire et demande du temps. Mais le message commence à passer, car beaucoup d’élèves procèdent bien de gauche à droite pour calculer mentalement 24,5 + 82,8.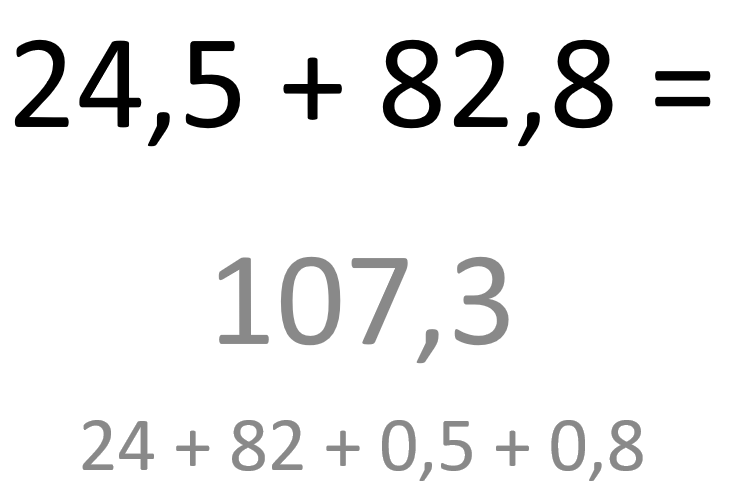
Dans le calcul de la différence 142,8 – 42,9 , la décomposition de 42,9 en 42,8 + 0,1 est une aide précieuse pour atteindre 99,9. Pour permettre aux élèves de comprendre et de corriger l’erreur classique 6,21 pour le calcul 3 × 2,7 , il est utile de rappeler que 3 × 2,7 , c’est aussi 2,7 + 2,7 + 2,7. Le passage par l’addition donne du sens à un calcul multiplicatif encore abstrait pour quelques élèves.

Le numérique : Calculatice et Chrono en salle multimédia

Le diaporama participe à la création d’une dynamique de classe et apporte de la régularité. Les échanges s’installent, on apprend par l’écoute des autres. Il y a une véritable dimension sociale dans la pratique du calcul mental réfléchi en classe. La découverte d’outils numériques va quant à elle permettre de prolonger de façon individuelle ces pratiques mentales.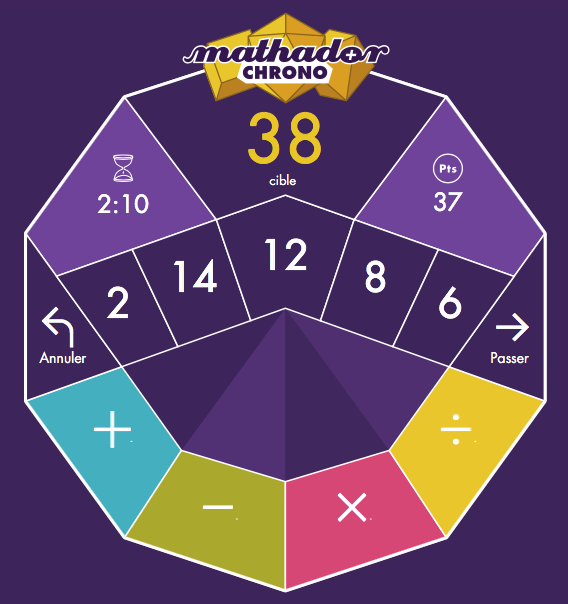

Mathador Chrono est le prolongement numérique des dés de Mathador Flash que l’on lance en classe. La présentation est rapide puisque le principe du jeu est connu avec les dés. En 3 minutes, il faut réaliser le plus de points possibles. On est alors dans un véritable entraînement qui va permettre de consolider des acquis et de découvrir par le test et le tâtonnement de nouveaux horizons. Les premières parties se font collectivement avec le TBI, mais on peut aussi commencer en salle multimédia, chacun ou en binôme sur son ordinateur. C’est un des apports du numérique : il favorise le travail de répétition, appelé aussi travail de gammes. Ce travail de gammes est indispensable, comme en sport ou en musique. Mais il est fastidieux et pas vraiment productif à l’écrit. L’association numérique et ludique a le pouvoir de rendre attractif ce type de travaux.

Une première séance en salle multimédia a permis à chaque élève de s’approprier le fonctionnement de Mathador Chrono. Avec la formule Mathador Classe qui fonctionne avec un abonnement, chaque élève a un identifiant et un mot de passe. Il pourra jouer sur tout support (ordinateur, tablette ou smartphone), aussi bien en classe qu’à la maison. Sur son compte, il aura ses statistiques et une galerie de trophées qu’il enrichira au fur et à mesure de ses parties.

Il y a également possibilité de faire des parties en réseau. Dans un premier temps, il faut être ami, façon réseaux sociaux ! Puis il s’agit de matchs entre 2 joueurs qui se déroulent en 3 manches. L’intérêt est que les tirages sont évidemment les mêmes et que les parties peuvent être jouées de façon asynchrone. Les joueurs sont avertis sur leur compte quand l’adversaire a terminé sa manche. Je termine chaque séance en salle multimédia par un quart d’heure de Mathador Chrono, les élèves ont le temps de faire environ 4 parties, ils ont leur feuille de scores pour noter, séance après séance, l’évolution de leurs scores et observer leur progression.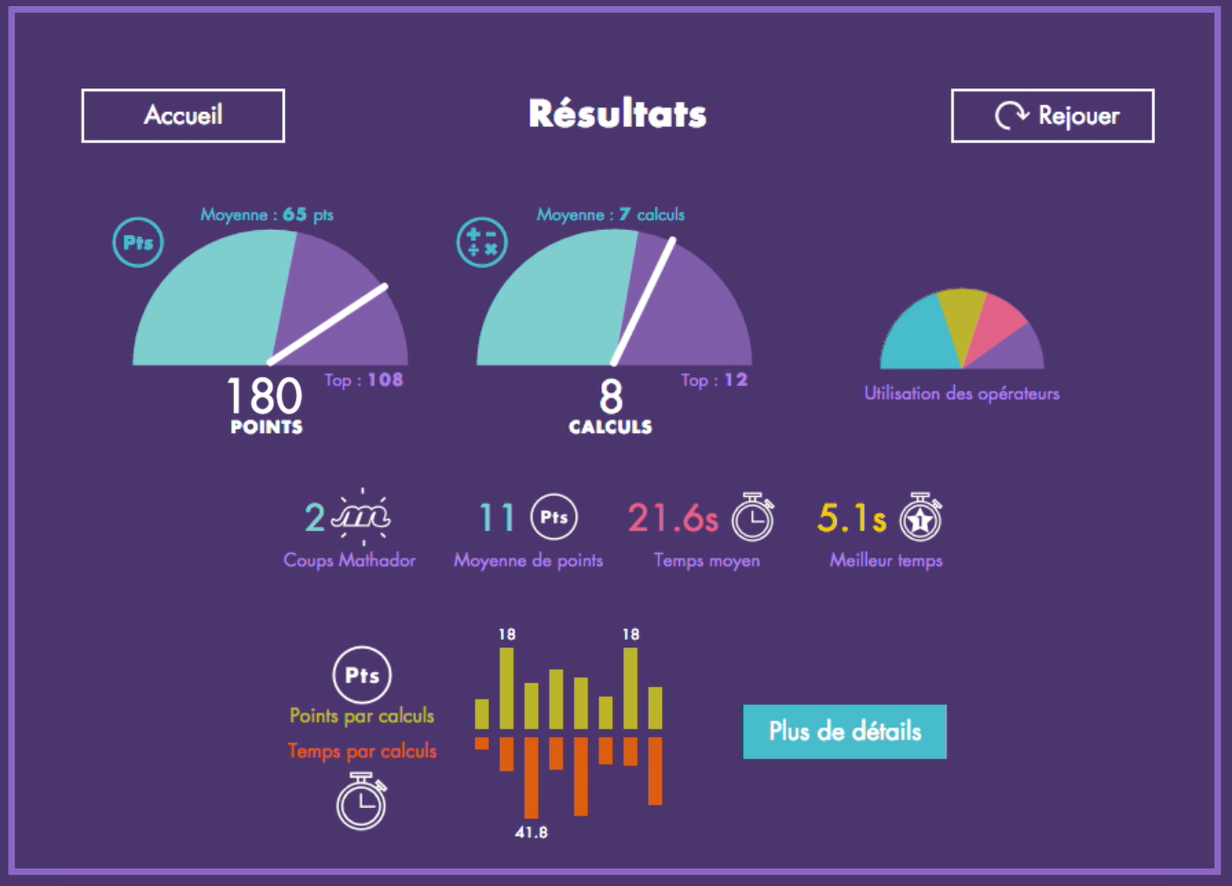
Ils vont pouvoir s’emparer de l’outil et le faire vivre dans d’autres lieux que la classe. Une véritable fréquentation des nombres et des opérations va pouvoir s’installer avec un rythme choisi. Le score réalisé lors d’une partie Mathador Chrono est une sorte de mesure d’aptitude en calcul mental. Son intérêt majeur réside dans le suivi. Plus qu’une mesure ponctuelle, c’est l’évolution des scores d’un élève qui va être intéressant. De quelques dizaines de points lors des premières parties, il va rapidement se stabiliser, en général entre 50 et 100 points. 50 points correspondent à un niveau moyen et 100 points est déjà un bon niveau avec un début de fluidité dans les calculs. La fréquence et la régularité sont ensuite des clés, qui dans la durée, vont permettre aux élèves de progresser et d’atteindre dans l’année, pour les meilleurs 200 points ou plus. L’ensemble des statistiques d’un élève, scores, mais aussi répartition des opérations choisies, nombres de calculs, durée pour les effectuer, sont à disposition de l’enseignant sur la plate-forme de suivi de la formule Mathador Classe. 

Lors d’une séance en salle multimédia, il est intéressant de prévoir une séquence jeu avec du calcul mental à l’envers, avec le quart d’heure Mathador Chrono comme évoqué plus haut, et du calcul mental à l’endroit. Le site Calculatice est une référence avec de nombreux jeux de calcul mental à l’endroit, il s’adresse aux élèves du CP à la 6°. Le principe du jeu de calcul avec l’outil numérique a de nombreux intérêts pédagogiques comme celui de s’adapter naturellement à l’élève puisque ce dernier gère son temps de réponse. L’élève peut donc se mettre à son rythme. Autre paramètre important, l’élève peut tester, se tromper plus facilement, il n’y a pas le regard direct des autres.

Dans la galerie de jeux sur le site Calculatice, succès garanti avec Quadricalc et Calcul@kart, deux jeux qui permettent d’entretenir et de consolider le répertoire des automatismes, type table. Avec les différents niveaux proposés, il est possible d’adapter au niveau de l’élève en partant d’additions simples jusqu’aux tables de multiplication.

Calcu@kart

Dans Calcu@kart, le joueur pilote une voiture de course. Sur le circuit, il y a régulièrement des camions qui apparaissent sur le circuit devant la voiture et sur chaque camion est inscrit une opération. Le joueur se voit proposer 4 réponses possibles et il doit tout simplement cliquer sur la bonne réponse pour pouvoir doubler le camion.

 

 

 

 

 

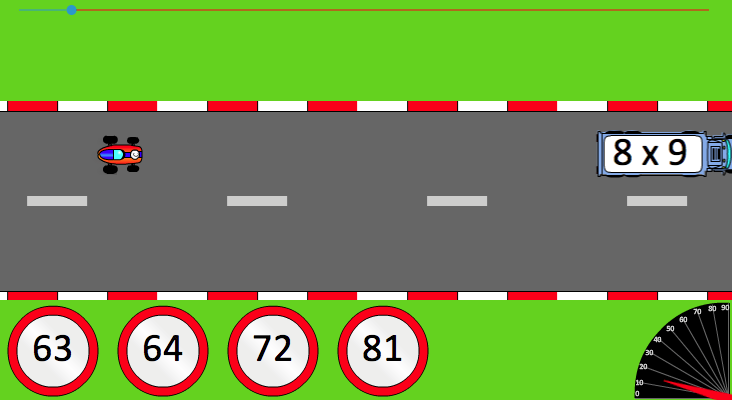
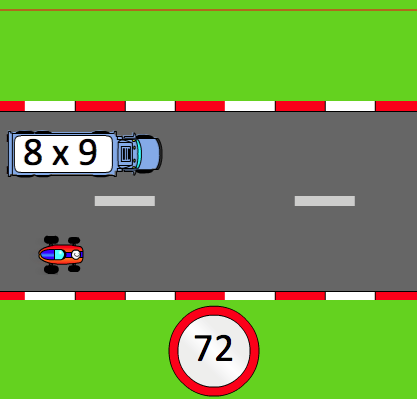
Et sinon, en cas d’erreur ou de réponse trop tardive, c’est l’accident et la voiture repart avec une vitesse au minimum. La bonne réponse est affichée pour que l’élève l’enregistre. Le but est évidemment d’avoir le maximum de bonnes réponses pour avoir le meilleur score possible. Suivant le niveau choisi, les opérations sont des additions ou des multiplications et la vitesse de la voiture est modulée.

Quadrilac

Quadricalc est tout simplement un « Tétris » avec des opérations. Il suffit, avec les flèches du clavier, de viser la bonne réponse lorsque la brique descend. Quadricalc se retrouve dans chaque niveau du CP à la 6^ème avec, à chaque fois, 4 niveaux de difficultés de vitesse de descente de la brique. Il est donc possible d’adapter à chacun le niveau de jeu avec les opérations travaillées, le registre additif ou multiplicatif. Bien sûr, c’est la régularité et la répétition de ce genre d’activités qui permet de consolider des résultats dans la durée. Associé au plaisir du jeu, le cocktail pédagogique fonctionne très bien. On retrouve dans ce type de jeux, un des intérêts du numérique : rendre attractif un travail de gammes qui, pratiqué de façon classique, peut devenir rapidement rébarbatif.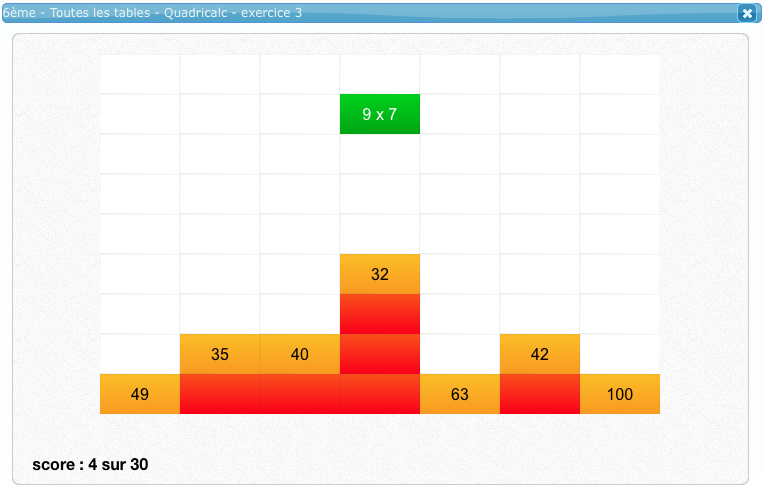
Bon jeu !