Calcul mental en classe : mode d’emploi

En ces temps de rentrée, je vous propose plusieurs outils pour vous aider à mettre en place une progression annuelle en calcul mental. Ces outils sont issus de ma pratique en collège, mais peuvent être transposés en élémentaire.

Mais avant de vous présenter ce mode d’emploi plus en détails, quelques constats et réflexions en lien avec l’enseignement du calcul mental !

• La mentalisation de la relation aux nombres et aux opérations doit être un préalable avant le passage à l’écrit et l’apprentissage des techniques opératoires : elle est fondamentale dans la construction de cette relation.
•   Manipulation et verbalisation devraient être des passages incontournables pour installer une mentalisation solide.
• Notre culture éducative occidentale nous pousse trop vite vers l’écrit, avec une phase mentale en amont trop faible voire absente. Le sens n’est pas encore installé que les procédures écrites sont en cours d’automatisation, alors qu’elles reposent bien souvent sur des bases mentales trop fragiles.
• Depuis une vingtaine d’années, les programmes évoluent dans le bon sens dans le domaine du calcul et intègrent une place de plus en plus grande au calcul mental et aux pratiques mentales. Il faut désormais construire cette culture mentale. Le récent rapport Villani-Torossian conforte cette place centrale du calcul et du calcul mental dans les programmes de l’école primaire et du collège.
• Il est important de sortir de l’image réductrice et fausse, calcul mental = apprentissage et mémorisation d’automatismes. Les automatismes sont à la fin du processus et n’ont d’utilité que de soulager la mémoire de travail de façon à pouvoir se consacrer à des tâches plus difficiles (notamment la résolution de problèmes qui reste l’activité centrale dans l’enseignement des mathématiques).
• C’est sur les bases de la pratique du calcul mental réfléchi que les automatismes vont progressivement se construire et se mémoriser.
• Ces pratiques mentales doivent se mettre en place tout au long des cycles 1, 2 et 3.
• Pour que le maximum d’élèves d’une classe puisse bénéficier des apports de ces pratiques mentales, il faut réunir plusieurs conditions : régularité, répétition et verbalisation par les élèves sont indispensables à une progression annuelle de calcul mental. La verbalisation lors de séquences de calcul mental réfléchi est l’occasion de mettre en lumière différentes procédures qui permettront de découvrir des propriétés des nombres et des opérations. Régularité et répétition sont indispensables pour les nombreux élèves qui ont besoin de temps pour construire cette mentalisation de la relation aux nombres et aux opérations. C’est particulièrement important pour les élèves qui n’ont pas suffisamment manipulé et joué avec les nombres dans leur cadre habituel de vie.

• Intégrer des jeux de calcul dans cette progression mentale apportera la touche de plaisir. Le jeu associé au numérique (applis ou logiciels ou sites internet) est une formidable possibilité pour donner à l’indispensable travail répétitif de gamme un caractère attractif.
• Ces grands principes sur l’enseignement du calcul mental sont en phase avec les paramètres soulignés par les neurosciences cognitives :
  attention de l’élève / susciter l’activité et la motivation de l’élève / retour rapide d’information / consolidation (régularité-répétition).

 

Voici 6 outils pour mettre en application les grands principes décrits ci-dessus. Cette liste n’est évidemment pas exhaustive : il existe désormais de très nombreux sites internet de collègues qui proposent des outils et des progressions pour enseigner  le calcul mental. C’est à chacun de choisir les outils qui lui conviennent et d’organiser sa progression comme il le souhaite !

1. Le diaporama : 2 à 3 fois par semaine

C’est un outil simple, pratique et efficace pour installer la régularité, la répétition et le plaisir du calcul mental.

Vous en trouverez de nombreux pour le cycle 3 téléchargeables sur le site de l’APMEP. J’utilise des diaporamas de 6 questions que vous retrouverez  dans la rubrique Progressions.

À chaque question, toujours laisser 10 à 20 secondes de recherche en silence et possibilité de lever la main si on pense avoir trouvé. Les élèves (volontaires ou désignés) proposent les réponses puis la validation est collective avec échanges sur les différentes méthodes quand il y en a. Cette verbalisation est importante en calcul mental réfléchi car l’élève va entendre des méthodes qu’il ne connaissait pas. La régularité et la répétition vont lui permettre d’enclencher dans la durée un processus de compréhension-mémorisation-utilisation.

Certains diaporamas sont pratiqués exclusivement à l’oral sans aucun écrit. D’autres, avec écrit sur le petit cahier calcul mental (petit cahier demandé dans la liste du matériel de mathématiques de mon collège). Dans ce cas, l’élève écrit la question du diaporama affichée au tableau puis sa réponse. Dans mes cours, je laisse 10 à 20 secondes de recherche par question, mais c’est à chaque professeur d’ajuster le temps de recherche en fonction de la question et du groupe en présence.

Tous les diaporamas contiennent les réponses aux questions : le retour pour l’élève est ainsi immédiat. Les neurosciences insistent sur l’importance du feedback si possible rapide.

Ils sont construits de la même manière : des questions de calcul mental automatisé, de calcul mental réfléchi et de calcul mental à l’envers.

C’est toujours une question-jeu en dernière position, avec une situation Trio ou Mathador : deux jeux avec un nombre-cible à fabriquer en utilisant des nombres donnés. Cette gymnastique est une clé dans la construction du sens du nombre et des opérations car l’élève est acteur : il doit choisir ses nombres et ses opérations ce qui, implicitement, lui fait travailler le sens. Pratiqué en parallèle du calcul mental classique à l’endroit, le calcul mental à l’envers est une gymnastique mentale puissante. Il faut la pratiquer régulièrement pour qu’elle donne des résultats durables. Du fait de l’utilisation de trois nombres seulement pour fabriquer le nombre-cible, Trio se prête bien à une pratique  exclusivement orale. Par contre, avec ses 5 nombres, Mathador est d’un niveau supérieur à Trio et nécessite l’écrit. Je demande aux élèves d’écrire leurs opérations (entre une et quatre) qui leur permettent de fabriquer le nombre-cible.
Pour les deux jeux, une fois la période de recherche achevée (de 1 à 2 min pour Trio et de 3 à 4 min pour Mathador), il est important que les élèves annoncent et verbalisent leurs solutions. Cela permet à chacun de découvrir d’autres techniques et procédures qui pourront être réutilisées ultérieurement. Pour Trio, souvent, je leur demande de m’indiquer sur la grille l’endroit du calcul et on le vérifie collectivement : indispensable car il y a parfois des erreurs. Pour Mathador, j’écris les lignes de calcul annoncées par l’élève ou parfois, ce sont eux qui viennent les écrire au tableau.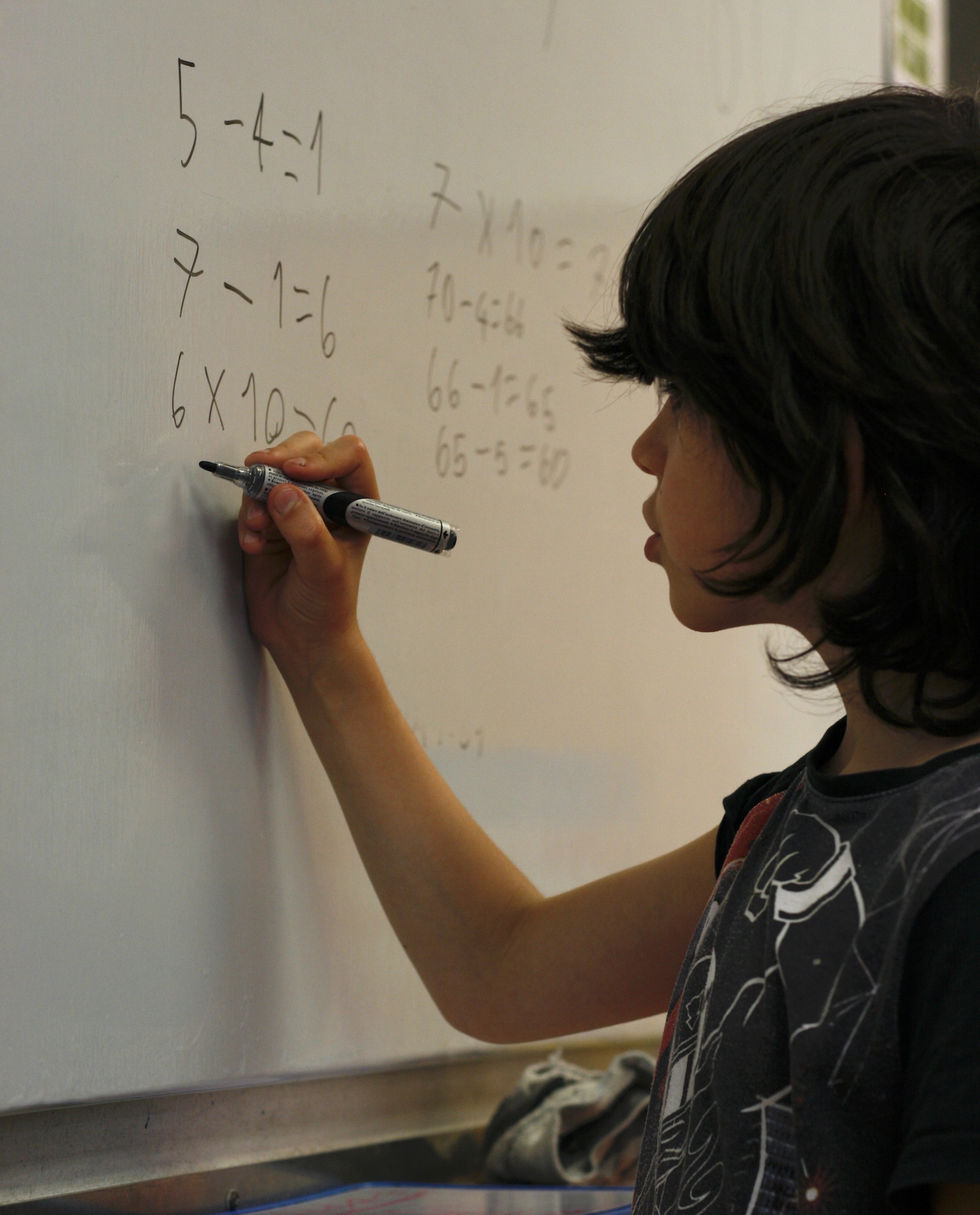

Le système de points de Mathador, détaillé dans la partie 6 et qui permet de différencier les solutions, sera introduit après quelques semaines de découverte du jeu et de pratique du calcul mental à l’envers, notamment avec le concours Mathador que je présente plus loin. Ce principe du calcul mental à l’envers étant non naturel, cela nécessite donc une indispensable période de rodage.

J’évalue quelquefois dans l’année mais peu souvent : je préfère insister sur l’auto-évaluation en les incitant à compter leurs bonnes réponses, de façon à entretenir l’envie et la spontanéité qui accompagne cette pratique et à favoriser la verbalisation et les échanges qui sont au cœur du processus.

 

2. Séance en salle multimédia : 2 fois par mois

Le travail sur ordinateur est idéal pour la mentalisation. Je travaille principalement la relation aux nombres et aux opérations. L’axe principal est le calcul mental avec Calculatice et Mathenpoche pour la partie calcul mental à l’endroit et Mathador et Trio pour la partie calcul mental à l’envers-jeu.

– J’utilise Mathenpoche pour l’échauffement des neurones ! => Numérique / entiers et opérations / calcul mental.
Il y a 15 exercices avec possibilité de n’en faire qu’une partie  : j’annonce aux élèves qu’ils peuvent passer au niveau suivant dès qu’ils ont 5 bonnes réponses de façon à accélérer l’échauffement.

– Calculatice est un excellent site pour consolider les connaissances de type table et pour certains de les apprendre. La dimension ludique est forte et associée au caractère répétitif, c’est très bon.
Dans le niveau 6°, il y a une palette de choix impressionnante. J’ai un faible pour la partie intitulé « Toutes les tables », notamment les jeux Quadricalc, Calcul@kart, Table attaque et Tri sélectif.
Je vous conseille de prendre le temps de les tester auparavant.

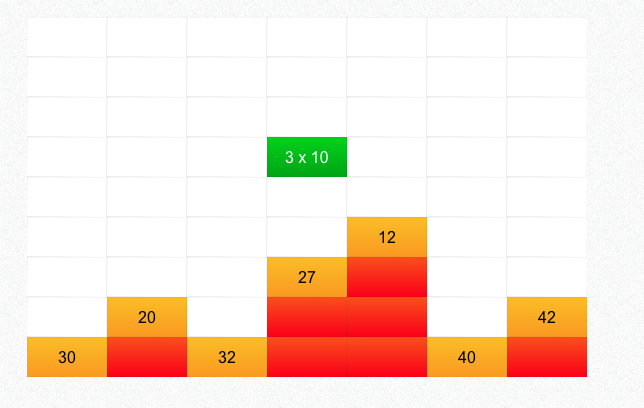
– J’utilise également le site jeuxmaths.fr sur lequel il y a de nombreux jeux très sympa. Notamment en géométrie, « Le bon angle » pour travailler la perception des mesures d’angles, « Vise le 1000 » pour travailler la perception de la symétrie axiale, « Le petit dragon (périmètre) » et « Le petit dragon (aire) ».

– Pour Trio, j’utilise aussi un site qui permet de jouer à Trio en ligne.

– Les séances en salle multimédia se terminent en général par 15’ de tournoi Mathador Chrono. Une partie dure 3 min et chacun essaye de faire le meilleur score avec le système de points associé aux opérations utilisées.

La régularité et la répétition sont encore une fois des clés pour des progrès en calcul mental. De façon à pouvoir mesurer ces progrès, je distribue à chaque élève une fiche de scores sur laquelle ils noteront tout au long de l’année l’évolution de leurs scores aux jeux de Calculatice et à Mathador Chrono. Pour le professeur de façon, cela permet de suivre cette évolution et d’apporter l’aide nécessaire. Pour ajouter un peu de défi et d’émulation positive, je leur permets de venir écrire leurs scores au tableau. Le côté compétition qu’on retrouve en sport est un levier sur lequel  je joue sans trop insister : il n’y a pas obligation de venir noter son score au tableau, chaque élève décide.

La pratique du jeu et du numérique a de multiples intérêts pédagogiques :
– elle améliore la mentalisation des concepts avant le passage à l’écrit en classe ;
– seul ou à deux, cela favorise le test et le tâtonnement car on a moins peur de se tromper ;
– elle créé un lien entre l’école et la maison car de nombreux élèves rejouent chez eux ;
– enfin, la dimension plaisir est essentielle lors de ces séances.

 

3. Le concours de calcul mental Mathador pour les classes

C’est un outil qui permet de proposer toutes les semaines de novembre à mai, un tirage hebdomadaire Mathador. Il installe une forme de régularité dans la pratique du calcul mental à l’envers, couplé avec la dimension ludique et le défi. Cette régularité hebdomadaire permet à chaque élève de progresser à son rythme sur l’année. La culture de la décomposition du nombre-cible peut s’installer. Il est intéressant de faire une rapide analyse du tirage de la semaine précédente pour montrer aux élèves différentes solutions et stratégies. Le fait de verbaliser et d’entendre de nouveaux chemins est une piste de progrès en calcul. D’autre part, le site du concours de Canopé permet un suivi statistique de la classe et de chaque élève.

C’est un instrument de mesure des évolutions et progrès de chaque élève en calcul mental. Ce concours, que je pratique depuis plusieurs années, créé une dynamique dans la classe et une émulation entre les élèves autour de la relation aux nombres et aux opérations. La particularité du concours Mathador et qui correspond à la règle de Mathador Flash, est un système de points qui incite à complexifier ses calculs afin d’avoir le maximum de points. Le détail de la règle est sur le site Mathador et vous le trouverez plus bas dans le point 6 de ce texte.

Les 3  points (diaporamas, salle multimédia et concours Mathador) forment la colonne vertébrale de ce projet de mise en place du mental au cœur de ma progression mathématique. Les points qui suivent sont complémentaires. Encore une fois, c’est à chacun, avec sa liberté pédagogique de se fabriquer son propre cocktail pédagogique.

 

4. Recherche en classe de petits problèmes uniquement en mental 

Pour poursuivre ce travail mental et le prolonger vers la résolution de problèmes !
Affichage de l’énoncé (court) au tableau ou au TBI, recherche silencieuse puis correction, avec verbalisation d’un élève et éventuellement échanges avec d’autres. Prolongement possible : recherche de petites énigmes, avec utilisation de l’écrit autorisé MAIS en évitant les techniques opératoires.

 

5. Décomposition d’un nombre suivant les 4 opérations

Encore un principe très simple à mettre en place dans la régularité d’une année scolaire : le professeur annonce un nombre à la classe et demande à chacun de le décomposer sous la forme d’une somme, puis d’une différence, puis d’un produit, et enfin d’un quotient.
On peut le pratiquer exclusivement à l’oral suivi d’une verbalisation avec sollicitation de plusieurs réponses pour chaque opération. Mais on peut aussi le pratiquer à l’écrit sur le petit cahier ou sur l’ardoise. Je pratique les deux. Si c’est un nombre décimal, l’écrit peut être nécessaire pour certains.

Il est important de solliciter plusieurs réponses pour bien mettre en évidence la diversité des chemins. C’est déjà un petit exercice de calcul mental à l’envers avec une création de décomposition dans la mesure où chacun doit « inventer » deux nombres à chaque étape. Vous serez surpris par quelques élèves en grande difficulté pour simplement choisir deux nombres. Difficulté due certainement due au formatage mental lié à une pratique trop souvent exclusive du calcul mental à l’endroit (un calcul annoncé et un résultat attendu). Autre intérêt pédagogique, travailler dans la durée l’apprentissage des 4 mots somme, différence, produit et quotient.

Enfin, ce petit exercice peut se pratiquer dans toutes les classes dès le CP et jusqu’en 4°-3° en jouant sur la taille et la famille du nombre à décomposer. C’est une excellente gymnastique des neurones !

 

6. Pour les créneaux de quelques minutes : Trio ou Mathador

Lorsque j’ai 5 ou 10 minutes devant moi, je dispose de deux pistes : soit une situation Trio de type diaporama que je vidéo-projette au tableau soit un lancer de dés Mathador.

Pour Trio, le fonctionnement est identique à un diaporama : 2 minutes de recherche puis les élèves qui pensent avoir trouvé proposent leurs solutions, exclusivement à l’oral.

Pour un lancer Mathador, les 7 dés sont lancés par 7 élèves différents. Lancer après lancer, du 4 faces au 20 faces puis les deux dés 10 faces, je note les nombres au tableau. Les élèves les écrivent sur leur petit cahier, sur une nouvelle page. 3 à 5 minutes de recherche, la consigne est de m’appeler à partir du moment où toutes les opérations sont écrites en ligne sur le cahier. Objectif : trouver une solution simple, dans un premier temps, puis essayer de la complexifier avec le plus de points possibles. Le système de points est le suivant : 5 pts dès que le nombre-cible est atteint puis on ajoute les points des opérations utilisées (+ 1pt, x 1 pt, – 2 pts et ÷ 3pts).

Le coup Mathador (utilisation des 5 nombres avec un +, un -, un x et un ÷) rapporte 18 points. Le système est conçu pour inciter l’élève à utiliser les opérations contraires (- et ÷) qui sont mentalement plus difficiles. Il est important de préciser aux élèves que l’objectif est d’abord de fabriquer le nombre-cible et que la complexification doit venir après. Certains élèves, en difficulté, n’ont pas les connaissances suffisantes pour rentrer dans une culture du choix, ce n’est possible qu’à partir d’une aisance mentale minimum. Après le temps de recherche, ce sont les élèves qui proposent leurs solutions, dans un premier temps, verbalement. J’essaye, le plus souvent possible, de noter au tableau 3 solutions différentes : une simple en 7 ou 8 pts, une moyenne autour de 10 pts et éventuellement un coup Mathador ou une solution complexe. Parfois, ce sont les élèves qui viennent les écrire au tableau. Ce principe de correction est très utile, notamment pour les élèves en difficulté. Cela permet de découvrir des stratégies, des chemins auxquels ils n’auraient pas pensé. Encore une fois, c’est la régularité et la répétition qui permettra les progrès. L’aléatoire du lancer des dés proposera parfois des situations difficiles voire impossible, la recherche collective le confirmera. Dans ce cas, on peut essayer de s’approcher au plus près du nombre-cible.

 

Pour résumer en quelques mot…

Faites du calcul mental le fil du conducteur du travail de l’année sur les nombres et les opérations. Le travail écrit (résolution de problèmes, exercices, cours, énigmes, …) vient se greffer dans le prolongement de cette construction mentale. C’est l’addition de tous les paramètres évoqués dans ce texte qui vont créer les conditions d’une véritable construction du sens du nombre et des opérations.

Si vous souhaitez plus de détails dans ce suivi, vous retrouverez sur le blog Mathador de nombreux billets sur la didactique du calcul mental, sur le suivi d’une classe ainsi que sur des jeux de calcul et des sites que j’évoque dans ce billet.

C’est à vous…