Le calcul mental en 6° – semaine 23

Aujourd’hui, je vous propose un zoom sur un exercice de décomposition d’un nombre cible ainsi que quelques conseils pratiques pour accroître l’efficacité du concours en classe !

Décomposition du nombre cible

Prenons comme exemple l’épreuve n°8 du cycle 3 :

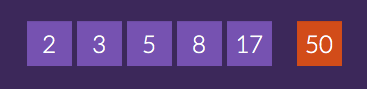
Un tirage intéressant car riche de nombreuses solutions ! Penchons nous sur les différentes décompositions de ce nombre cible. Il est très intéressant de présenter à la classe ce type d’analyse pour ouvrir des perspectives nouvelles dans la tête de nos élèves. Les études montrent en effet qu’un être humain a tendance à reproduire les mêmes stratégies en calcul, d’où l’importance de procéder en classe à une analyse des différents chemins possibles d’un tirage de façon à proposer des chemins différents.

La répétition de ces analyses conjuguée à l’enchaînement hebdomadaire des tirages du concours donne alors la possibilité de mettre en application ces idées nouvelles !

Revenons à notre nombre 50 pour lequel deux pistes de décompositions multiplicatives viennent rapidement  à l’esprit : 5×10 ou 2×25. Ces deux décompositions sont utiles pour trouver une solution simple.
Je le répète à chaque tirage : « Cherchez une solution simple avant de rentrer dans des chemins plus complexes ! »

Exemple de solutions simples :

• 8+2=10 puis 5×10=50 ou 17+8=25 et 25×2=50. Voilà deux solutions simples qui rapportent 7 points.

Concernant les chemins plus complexes pour ce tirage n°8  :

• D’autres pistes de 5×10 : 5 étant donné, il suffisait de fabriquer un 10 : 3-2=1 ; 17-8=9 ; 9+1=10 puis 5×10=50 rapporte 11 points.
• Ou un enchaînement de 3 soustractions permettaient d’obtenir 12 points : 3-2=1 ; 8-1=7 ; 17-7=10 puis 5×10=50.

Un des intérêts pédagogiques du principe de Mathador réside dans le principe de tester et tâtonner pour atteindre ce nombre-cible. Soit, comme dans les exemples ci-dessus, le nombre-cible est fabriqué à partir d’une décomposition multiplicative type 5×10 ou 2×25, soit des approches supérieures ou inférieures à la cible permettent d’atteindre ensuite cette cible. C’est alors l’occasion de mobiliser ses connaissances automatisées autour du nombre-cible et d’en tester des nouvelles. La répétition et la régularité des situations permettent alors, dans la durée, de fabriquer de nouveaux automatismes. Dans la situation présente, c’est la table du 5 qui peut être sollicitée avec 5×8 ou 5×9 avec un 9 fabriqué. Mais il y a aussi 17×3 que quelques élèves commencent à mémoriser. Le début des tables de 12 à 19 est un bon exemple de ces résultats non appris mais que la répétition et la régularité des situations Mathador va permettre, avec le temps, de mémoriser. À titre personnel, j’ai automatisé le début des tables de 12 à 19 sans jamais avoir fait l’effort de les mémoriser. C’est la répétition des lancer de l’icosaèdre qui en est la cause : merci le dé à 20 faces !

Basé sur 5×8, j’ai lu cette solution :

• 5×8=40 ; 17+3=20 ; 20 :2=10 et 40+10=50 rapporte 11 points.
• Basé sur 5×9, j’ai lu cette solution : 17-8=9 ; 5×9=45 ; 45+3=48 et 48+2=50 rapporte 10 points.

Par contre, j’ai eu l’agréable surprise de découvrir 3 solutions différentes à partir de 17×3 dont un coup Mathador, les voilà :

• 17×3=51 ; 8-5=3 ; 3-2=1 et 51-1=50 rapporte 12 points
• 17×3=51 ; 8:2=4 ; 5-4=1 et 51-1=50 rapporte 13 points

Cette dernière solution est très proche d’un coup Mathador. Il faut maîtriser l’idée que deux soustractions successives peuvent se transformer en une addition et une soustraction, une bonne préparation aux propriétés calculatoires avec les parenthèses précédées d’une soustraction.

Voilà ce coup Mathador qui rapporte 18 points :

• 17×3=51 ; 8:2=4 ; 51-5=46 et 46+4=50

À noter qu’il y avait un autre coup Mathador possible. Le paradoxe est qu’il était, à priori plus simple, mais je ne l’ai pas trouvé parmi mes deux classes de 6° :

• 8:2=4 ; 4+3=7 ; 17-7=10 et 10×5=50

Conseils pratiques pour accompagner le tirage hebdomadaire

Lors de la distribution de la feuille de score sur laquelle l’élève va écrire ses calculs, il est intéressant de donner en même temps la feuille de scores de la semaine précédente. Si, en plus, vous venez de faire une analyse des différentes solutions au tableau, chaque élève aura l’occasion de confronter ses choix avec vos propositions. C’est un moment important pour mémoriser des stratégies de calculs que l’élève pourra mettre à profit lors des prochains tirages.

Autre conseil pratique dont j’ai mesuré l’importance avec le temps, le fait de conseiller aux élèves de noter plusieurs solutions sur leur feuille pour valider éventuellement celle qui donnera le plus de points.  Un autre avantage, constaté régulièrement, c’est aussi une bonne stratégie pour éviter un zéro en cas d’erreur dans un calcul ! Nul n’est à l’abri d’une erreur « bête » de calcul en raison du manque de temps ou du stress lié à la gestion de ce temps. Si l’élève a prévu plusieurs solutions, il pourra se permettre parfois l’erreur d’étourderie sans conséquence sévère.

Le lancer de dés

Le tirage hebdomadaire du concours est un bon outil pour construire une progression annuelle de calcul mental avec de la régularité. Pour être efficace pédagogiquement, il doit être accompagné par d’autres outils. Les diaporamas de calcul mental font partie de ce fil conducteur annuel, les séances en salle multimédia avec « Mathenpoche », « Calculatice » ou encore « Mathador Chrono » également.
Le lancer de dés par les élèves a toute sa place dans ce dispositif d’enseignement du calcul mental. Le mode d’emploi détaillé est à retrouver dans le billet 4.
La particularité du lancer de dés est de mettre tout le monde à égalité, le professeur va également découvrir le résultat du lancer en même temps que la classe. Les élèves apprécient ce moment avec le mystère de découvrir les nombres les uns après les autres par le lancer de chaque dé par un élève différent. Certains tirages donnent des situations difficiles voire parfois impossible. Mais, il est intéressant d’un point de vue pédagogique de se trouver face à une situation non prévue et pour laquelle une vraie recherche approfondie permettra de conclure. La multiplication des tests opératoires mêlée à la manipulation des ordres de grandeur est très riche et participe à la construction dans la durée de ce sens des nombres et des opérations.