Le calcul mental en 6°- semaine 29

En ce début de 3^ème trimestre, toutes les activités mentales habituelles se poursuivent. Je vais revenir  sur les dernières séries de calcul mental et les derniers tirages du concours Mathador.

Attardons nous tout d’abord sur la proportionnalité et les pourcentages…

Proportionnalité et pourcentages

L’aisance en calcul mental se vérifie particulièrement bien dans un domaine : la proportionnalité. Je commence mes séances sur la proportionnalité par des petites situations de la vie courante de façon orale et mentale comme : « Quatre gâteaux coûtent 10€, quel est le prix de 6 gâteaux ? Puis 5 gâteaux ? » La mise en évidence du passage à l’unité, le prix d’un gâteau, est importante et la gestion mentale des quatre opérations et de leur sens est alors essentielle. Je mesure les progrès notamment pour des élèves qui étaient en difficultés avec les nombres en début d’année et qui ont réellement progressé. L’aisance en calcul mental diffuse un ressenti, un sens plus fort pour chaque opération.

Les situations proposent aussi des pourcentages. Un exemple fonctionne bien : dans un collège de 600 élèves, je leur demande de trouver un nombre d’élèves à travers six à huit cas différents avec une progression dans la difficulté. La réponse est donnée et expliquée à chaque fois par un élève. Exemples : 50% des élèves apprennent l’anglais, cela fait combien d’élèves ? ; 25% apprennent l’espagnol, cela fait combien d’élèves ? ; 75% sont demi-pensionnaires puis 10% apprennent l’italien… ; 7% apprennent le grec… et ainsi de suite. Il faut alors bien présenter le fonctionnement du passage à l’unité et son utilité pour la suite ; Je termine par une petite note humoristique et astucieuse du style, 99% des élèves aiment les frites, cela fait combien d’élèves ?

Cette situation est proposée pendant trois séances de façon à pouvoir mémoriser et tendre vers une automatisation de certaines procédures comme par exemple les liens entre 50% et la moitié, 25% et le quart, 75% et les trois-quarts ou 10% et le dixième. Par contre, je modifie à chaque séance le nombre d’élèves du collège pour que les calculs changent tout en travaillant les mécanismes mentaux. La première séance sera avec 600 élèves, puis 800 et enfin 900 élèves.

Retour sur les séries de calcul mental 

Dans la 27-6° à l’oral : les trois premières questions sur l’addition, la soustraction et la multiplication mettent en situation des nombres décimaux et mêlent la maîtrise de la numération décimale avec un véritable sens de ces opérations. Il est important qu’un élève de fin de cycle 3 sache gérer mentalement les trois opérations suivantes :

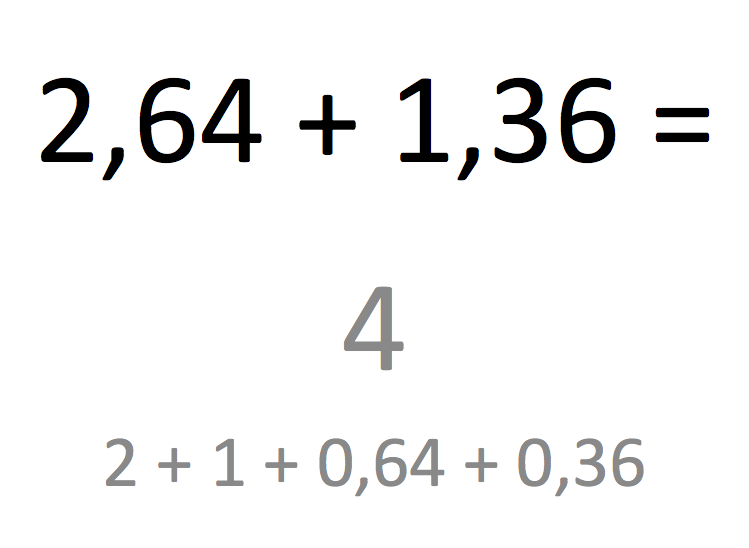
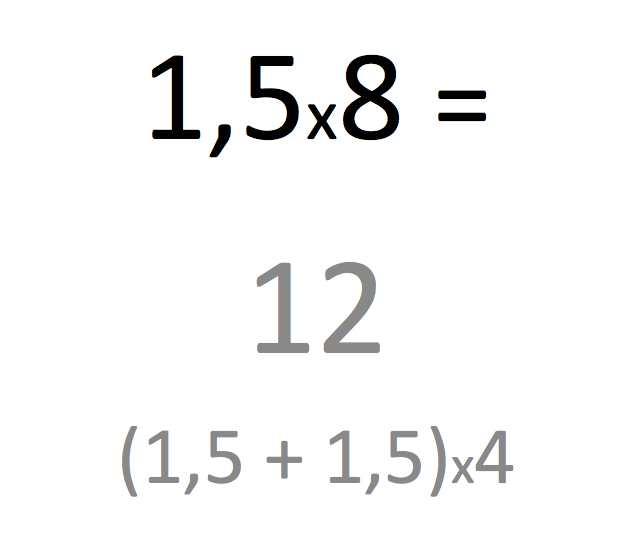La 4^ème diapo de cette série 27 sur la division est l’occasion d’insister encore sur la liaison forte des 4 opérations entre elles avec le principe des opérations contraires « + » et « – » ainsi que « x » et « : ». Le registre mental est idéal pour bien mettre en avant ces liaisons contraires en insister sur le fait qu’une soustraction peut toujours se gérer comme un complément avec une addition, de même que pour la division avec un tâtonnement de type multiplicatif. Cela fonctionne très bien pour :

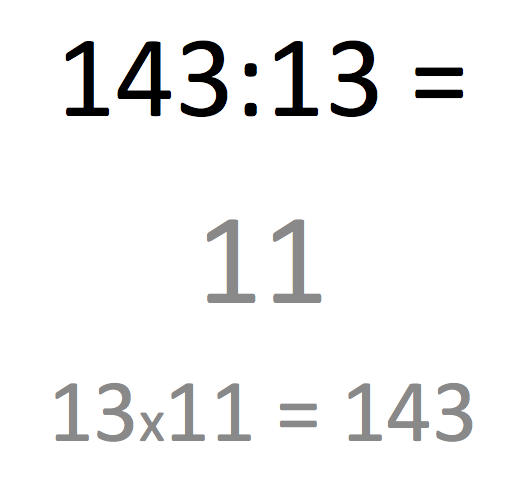
Et encore mieux dans la diapo suivante à la façon du commerçant qui rend la monnaie sur un billet de 20€ : 5 centimes qui font 14 et 1€ qui font 15 et 5€ qui font 20, soit 6,05€.

Dans la 28-6° à l’écrit : à noter les intéressantes solutions proposées pour le calcul de 24×25. Les premières basées sur la distributivité avec 10×25+10×25+4×25 mais aussi 20×25+4×25 pour ceux qui ont automatisés que 20×25=500. Une proposition basée sur une vision de 25 comme le quart de 100 qui donne (24×100):4 mais aussi une proposition basée sur la décomposition multiplicative de 24 en 6×4 qui donne 24×25=6x4x25 et 600 apparaît presque naturellement en 6×100. Un élève a également proposé 25×25-25=625-25, il avait automatisé le carré de 25 en 625. Ce 24×25 est un exemple supplémentaire de la richesse de la pratique de la recherche en classe de situations de calcul mental réfléchi. La verbalisation des procédures par les élèves et les échanges permettent à chacun de s’enrichir et d’apprendre par l’écoute des autres, une dimension sociale très intéressante du calcul mental réfléchi.

Dernière ligne droite du concours ! 

Nous vivons déjà les deux derniers tirages de ce 3^ème concours national. Je mesure l’apport de cet outil concours pour travailler la décomposition des nombres de façon régulière. Tous mes élèves de 6° sont rentrés dans cette culture de la décomposition qui est au cœur du sens des nombres et des opérations.
Avant-dernier tirage du cycle 3 :

De nombreux élèves ont proposé en décomposition simple 5×11+15 ou (2×5)x(11-4), solutions en 7 et 9 points. Le coup Mathador axé sur 7×10 n’était pas facile avec l’idée du 10 fabriqué avec (15+5):2  puis multiplié à 11-4 pour atteindre 70.

Dernier tirage du cycle 3 :

En décomposition simple, j’ai beaucoup lu : 3×15+12 et 4×15-3, solutions en 7 et 8 points. Très heureux d’avoir corrigé deux coups Mathador différents avec 4×15 – 7 + (12:3) et également un coup Mathador basé sur la table du 19 car 57=3×19 avec (15+4)x(7 – (12:3)). L’élève qui en est l’auteur, a fait des progrès étonnants en calcul mental tout au long de l’année. Il a désormais une aisance remarquable avec les nombres et les opérations et il excelle dans tous les domaines numériques des mathématiques. Il reconnaît lui-même avoir automatisé des résultats des tables du 12 ; 13 ; 14 … jusqu’à 19 avec la régularité et la répétition de Mathador sur l’ensemble de l’année scolaire. Voilà une bonne nouvelle qui confirme que l’automatisation peut se faire par la répétition et la régularité des situations et sans un apprentissage par cœur !

Pour finir, un moment fort dans une de mes deux classes de 6° : la venue d’une équipe de journalistes du magazine Le Point pour un reportage dans le cadre d’un numéro hors-série sur le calcul mental !

Bonne fin de concours à tous !